CWGI Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 4 wersji utworzonych przez 2 użytkowników) | |||
| Linia 15: | Linia 15: | ||
Metoda I (za pomocą przekroju)''' | Metoda I (za pomocą przekroju)''' | ||
Przez punkty '''A''' i '''B''' prowadzimy płaszczyznę pionowo - rzutującą <math> \varphi''</math>, która jest równoległa do rzutni poziomej. Tak poprowadzona płaszczyzna wyznaczy nam przekrój walca w postaci okręgu, równoległego do rzutni poziomej, którego dwie średnice wzajemnie prostopadłe oznaczymy w rzucie pionowym jako <math>P''Q'</math>' i <math>R''S''</math>. Jedna ze średnic <math>PQ</math> będzie równoległa do rzutni pionowej, druga <math>RS</math> do niej prostopadła. W rzucie pionowym otrzymamy, zatem średnicę <math>P''Q''</math> w wielkości rzeczywistej oraz średnicę <math>R''S''</math>, która będzie punktem. Rzutem poziomym przekroju (okręgu) będzie okrąg pokrywający się z rzutem poziomym walca. Bez trudu na rzucie poziomym przekroju można wyznaczyć rzuty poziome średnic <math>P'Q'</math> i <math>R'S'</math> przekroju walca płaszczyzną <math>\varphi''</math>. Na przekroju w postaci okręgu wyznaczymy poszukiwane rzuty poziome punktów <math>A'</math> i <math>B'</math>. W celu oznaczenia widoczności punktów w rzucie pionowym prowadzimy pomocniczą płaszczyznę <math>\gamma'</math>, która określa widoczną część powierzchni walca. Wszystkie punkty leżące poniżej tej płaszczyzny są widoczne, natomiast powyżej są niewidoczne. Z przeprowadzonej analizy wynika, zatem, że punkt <math>A\ | Przez punkty '''A''' i '''B''' prowadzimy płaszczyznę pionowo - rzutującą <math>\varphi''</math>, która jest równoległa do rzutni poziomej. Tak poprowadzona płaszczyzna wyznaczy nam przekrój walca w postaci okręgu, równoległego do rzutni poziomej, którego dwie średnice wzajemnie prostopadłe oznaczymy w rzucie pionowym jako <math>P''Q'</math>' i <math>R''S''</math>. Jedna ze średnic <math>PQ</math> będzie równoległa do rzutni pionowej, druga <math>RS</math> do niej prostopadła. W rzucie pionowym otrzymamy, zatem średnicę <math>P''Q''</math> w wielkości rzeczywistej oraz średnicę <math>R''S''</math>, która będzie punktem. Rzutem poziomym przekroju (okręgu) będzie okrąg pokrywający się z rzutem poziomym walca. Bez trudu na rzucie poziomym przekroju można wyznaczyć rzuty poziome średnic <math>P'Q'</math> i <math>R'S'</math> przekroju walca płaszczyzną <math>\varphi''</math>. Na przekroju w postaci okręgu wyznaczymy poszukiwane rzuty poziome punktów <math>A'</math> i <math>B'</math>. W celu oznaczenia widoczności punktów w rzucie pionowym prowadzimy pomocniczą płaszczyznę <math>\gamma'</math>, która określa widoczną część powierzchni walca. Wszystkie punkty leżące poniżej tej płaszczyzny są widoczne, natomiast powyżej są niewidoczne. Z przeprowadzonej analizy wynika, zatem, że punkt <math>A\ </math>, w rzucie pionowym będzie niewidoczny. | ||
''' | ''' | ||
Metoda II (za pomocą tworzących)''' | Metoda II (za pomocą tworzących)''' | ||
| Linia 30: | Linia 30: | ||
|valign="top" width="500px"|[[Grafika:CWGI_M5_Slajd3.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M5_Slajd3.png]] | ||
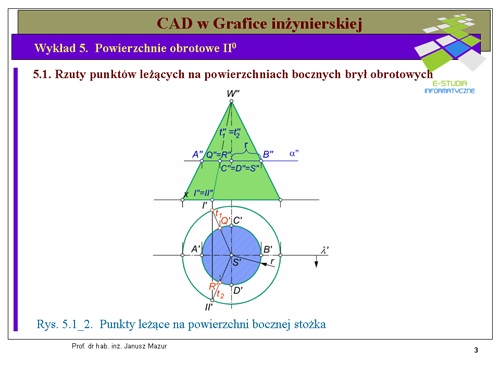
|valign="top"|Podobną konstrukcję ustalania rzutów punktów, tym razem <math>QR</math>, przedstawiono na rys. 5-1_2 | |valign="top"|Podobną konstrukcję ustalania rzutów punktów, tym razem <math>QR</math>, przedstawiono na rys. 5-1_2 | ||
w odniesieniu do powierzchni stożka. Zarówno metoda przekroju płaszczyzną <math>\alpha''</math> jak i metoda tworzących przyniosła oczekiwany efekt. W wyniku przekroju płaszczyzną <math>\alpha\ | w odniesieniu do powierzchni stożka. Zarówno metoda przekroju płaszczyzną <math>\alpha''</math> jak i metoda tworzących przyniosła oczekiwany efekt. W wyniku przekroju płaszczyzną <math>\alpha\ </math>,, przechodzącą przez rzuty pionowe punktów leżących na powierzchni bocznej stożka otrzymamy okrąg, który bez zniekształceń w rzucie poziomym. Na okręgu tym leżą rzuty poziome punktów <math>Q'R'</math>. Konstrukcję powtarzamy prowadzac w rzucie pionowym tworzące stożka przechodzące przez rzuty pionowe punktów <math>Q''\i\R''</math>. Rzuty poziome tych punktów będą leżały na rzutach poziomych tworzących oraz na odnoszących rzutowania prostokątnego. Granicą widoczności dla rzutu pionowego jest płaszczyzna poziomo – rzutująca równoległa do płaszczyzny pionowej.<math>\gamma’</math>. Z analizy widoczności punktów na powierzchni stożka wynika, że punkt '''Q''' w rzucie pionowym będzie niewidoczny, natomiast punkt '''R''' będzie widoczny. | ||
| Linia 40: | Linia 40: | ||
|valign="top" width="500px"|[[Grafika:CWGI_M5_Slajd4.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M5_Slajd4.png]] | ||
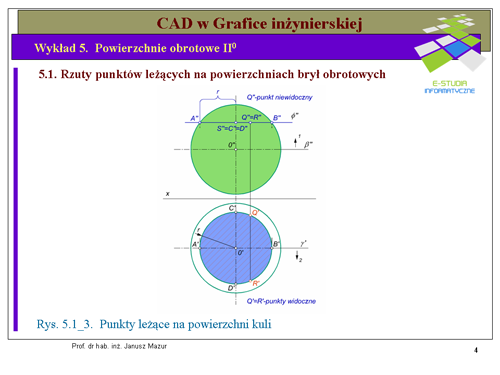
|valign="top"|Wyznaczanie punktów leżących na powierzchni kuli realizowane jest za pomocą metody przekroju płaszczyzną, przechodzącą przez analizowane punkty, równoległą do rzutni poziomej. Metoda druga nie jest wykorzystywana z takiego względu, iż w miejsce tworzących musielibyśmy wprowadzić południki, które w rzutach na ogół są elipsami, trudnymi do pełnej, precyzyjnej konstrukcji. W geometrii znana jest siatkowa metoda wyznaczania elipsy określonej przez dwie średnice sprzężone, ale jest to jednak metoda przybliżona. Skorzystamy, zatem z metody przekroju, albowiem jest ona w tym przypadku precyzyjna i nie powoduje żadnych niejednoznaczności. Przyjmijmy rzuty pionowe punktów <math>Q''</math> i <math>R''</math> leżących na powierzchni kuli. Wyznaczenie rzutów poziomych punktów nie powinno mam sprawić żadnych trudności. Jest to konstrukcja podobna jak w przypadku walca | |valign="top"|Wyznaczanie punktów leżących na powierzchni kuli realizowane jest za pomocą metody przekroju płaszczyzną, przechodzącą przez analizowane punkty, równoległą do rzutni poziomej. Metoda druga nie jest wykorzystywana z takiego względu, iż w miejsce tworzących musielibyśmy wprowadzić południki, które w rzutach na ogół są elipsami, trudnymi do pełnej, precyzyjnej konstrukcji. W geometrii znana jest siatkowa metoda wyznaczania elipsy określonej przez dwie średnice sprzężone, ale jest to jednak metoda przybliżona. Skorzystamy, zatem z metody przekroju, albowiem jest ona w tym przypadku precyzyjna i nie powoduje żadnych niejednoznaczności. Przyjmijmy rzuty pionowe punktów <math>Q''</math> i <math>R''</math> leżących na powierzchni kuli. Wyznaczenie rzutów poziomych punktów nie powinno mam sprawić żadnych trudności. Jest to konstrukcja podobna jak w przypadku walca | ||
i stożka. Przekrojem kuli płaszczyzna <math>\alpha''</math> będzie okrąg, który w rzucie pionowym jest odcinkiem, natomiast w rzucie poziomym jest okręgiem o niezmienionej wielkości. Rzut poziomy tego okręgu wyznaczymy ustalając jego promień <math>r\ | i stożka. Przekrojem kuli płaszczyzna <math>\alpha''</math> będzie okrąg, który w rzucie pionowym jest odcinkiem, natomiast w rzucie poziomym jest okręgiem o niezmienionej wielkości. Rzut poziomy tego okręgu wyznaczymy ustalając jego promień <math>r\ </math>, w rzucie pionowym. Na rzucie poziomym okręgu znajdziemy poszukiwane rzuty poziome punktów <math>Q'</math> i <math>R'</math>. | ||
| Linia 48: | Linia 48: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:CWGI_M5_Slajd5.png]] | ||
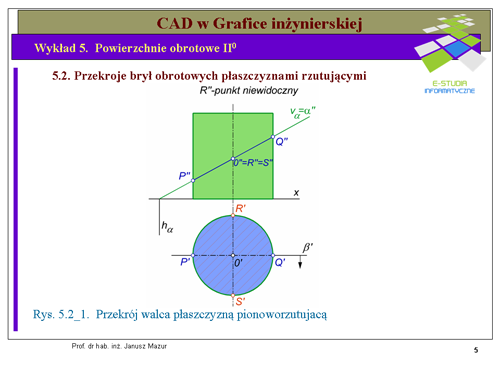
|valign="top"|Przekrojami brył obrotowych są krzywe stopnia II, takie jak elipsa, okrąg, parabola lub hiperbola. Najczęściej mamy do czynienia z przekrojami w postaci okręgu lub elipsy. Zwykle rzutem równoległym okręgu jest elipsa. Zatem skupimy się na tej krzywej, wyznaczając przekroje podstawowych brył obrotowych II stopnia, z jakimi mamy do czynienia w technice. Okrąg będziemy definiowali podając dwie średnice wzajemnie prostopadłe. Taka definicja pozwala ustalić środek okręgu oraz jego promień, jest ona wygodna, gdy będziemy definiować elipsę. | |valign="top"|Przekrojami brył obrotowych są krzywe stopnia II, takie jak elipsa, okrąg, parabola lub hiperbola. Najczęściej mamy do czynienia z przekrojami w postaci okręgu lub elipsy. Zwykle rzutem równoległym okręgu jest elipsa. Zatem skupimy się na tej krzywej, wyznaczając przekroje podstawowych brył obrotowych II stopnia, z jakimi mamy do czynienia w technice. Okrąg będziemy definiowali podając dwie średnice wzajemnie prostopadłe. Taka definicja pozwala ustalić środek okręgu oraz jego promień, jest ona wygodna, gdy będziemy definiować elipsę. | ||
| Linia 64: | Linia 64: | ||
|valign="top" width="500px"|[[Grafika:CWGI_M5_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M5_Slajd6.png]] | ||
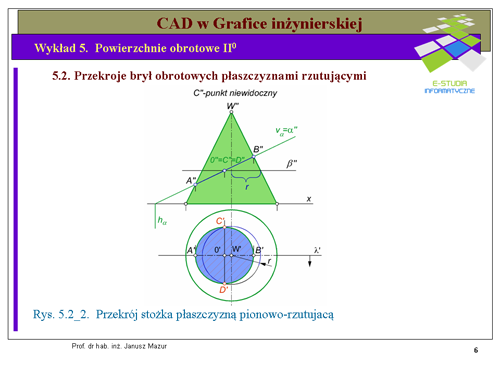
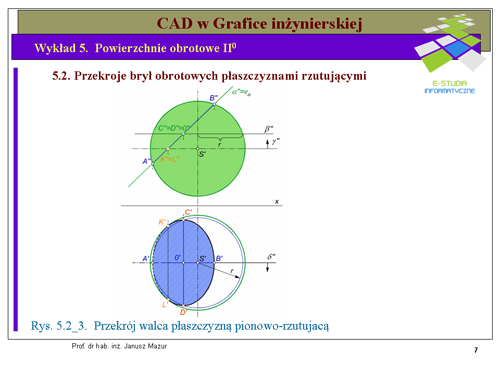
|valign="top"|'Kolejnym przykładem przekroju bryły obrotowej płaszczyzną rzutującą jest przekrój stożka. Przyjmijmy założenia do niniejszego zadania zgodnie z rys. 5.2_2. Stożek prosty stoi na rzutni poziomej. Płaszczyzna krojąca opisana została literą <math>\alpha''</math>. Przekrojem stożka w tym przypadku jest elipsa, której osie główne (wzajemnie prostopadłe), podobnie jak w przypadku walca są odpowiednio: <math>AB</math> - równoległa do rzutni pionowej oraz <math>CD</math> prostopadła do rzutni pionowej. | |valign="top"|'Kolejnym przykładem przekroju bryły obrotowej płaszczyzną rzutującą jest przekrój stożka. Przyjmijmy założenia do niniejszego zadania zgodnie z rys. 5.2_2. Stożek prosty stoi na rzutni poziomej. Płaszczyzna krojąca opisana została literą <math>\alpha''</math>. Przekrojem stożka w tym przypadku jest elipsa, której osie główne (wzajemnie prostopadłe), podobnie jak w przypadku walca są odpowiednio: <math>AB</math> - równoległa do rzutni pionowej oraz <math>CD</math> prostopadła do rzutni pionowej. | ||
Rzutem pionowym tych osi będą średnice sprzężone wzajemnie prostopadłe. Krańcowe punkty osi <math>A''</math> i <math>B''</math> wyznaczymy metodą tworzących. Tworzące skrajne w rzucie pionowym, na których leżą punkty <math>A''</math> i <math>B''</math> rzutują się w rzucie poziomym na oś poziomą rzutu stożka. Na rzutach poziomych tych tworzących wyznaczymy rzuty punktów <math>A'</math> i <math>B'</math>. Punkty <math>C\ | Rzutem pionowym tych osi będą średnice sprzężone wzajemnie prostopadłe. Krańcowe punkty osi <math>A''</math> i <math>B''</math> wyznaczymy metodą tworzących. Tworzące skrajne w rzucie pionowym, na których leżą punkty <math>A''</math> i <math>B''</math> rzutują się w rzucie poziomym na oś poziomą rzutu stożka. Na rzutach poziomych tych tworzących wyznaczymy rzuty punktów <math>A'</math> i <math>B'</math>. Punkty <math>C\ </math>, i <math>D\ </math>, należące przecież do powierzchni bocznej stożka wyznaczymy metodą przekroju płaszczyzną <math>\beta''</math>, równoległą do rzutni poziomej w wyniku, którego otrzymamy w rzucie poziomym okrąg o promieniu '''r'''. Konstrukcję tą przedstawiono już rozwiązując zagadnienia na tym wykładzie. Punkt <math>C''</math> zarysu przekroju zgodnie z wcześniejszymi analizami jest niewidoczny, pozostałe punkty należące do osi są widoczne. | ||
| Linia 74: | Linia 74: | ||
|valign="top" width="500px"|[[Grafika:CWGI_M5_Slajd7.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M5_Slajd7.png]] | ||
|valign="top"|Kula jest kolejną bryłą, dla której wyznaczymy przekrój płaszczyzną pionowo rzutującą <math>\alpha''</math>. Przekrojem kuli jest oczywiście okrąg, którego średnice wzajemnie prostopadłe są odpowiednio: <math>AB</math> - równoległa do rzutni pionowej oraz <math>CD</math> prostopadła do rzutni pionowej (rys.5.2_2). | |valign="top"|Kula jest kolejną bryłą, dla której wyznaczymy przekrój płaszczyzną pionowo rzutującą <math>\alpha''</math>. Przekrojem kuli jest oczywiście okrąg, którego średnice wzajemnie prostopadłe są odpowiednio: <math>AB</math> - równoległa do rzutni pionowej oraz <math>CD</math> prostopadła do rzutni pionowej (rys.5.2_2). | ||
Punkty <math>A''</math> i <math>B''</math> znajdują się na rzucie pionowym głównego południka, który w rzucie poziomym rzutuje się w postaci odcinka leżącego na osi poziomej kuli. Możemy, zatem bez trudu wyznaczyć rzuty poziome punktów <math>A'</math> i <math>B'</math>. Rzuty poziome punktów <math>C\ | Punkty <math>A''</math> i <math>B''</math> znajdują się na rzucie pionowym głównego południka, który w rzucie poziomym rzutuje się w postaci odcinka leżącego na osi poziomej kuli. Możemy, zatem bez trudu wyznaczyć rzuty poziome punktów <math>A'</math> i <math>B'</math>. Rzuty poziome punktów <math>C\ </math>, i <math>D\ </math>, należące do powierzchni bocznej kuli wyznaczymy metodą przekroju płaszczyzną <math>\beta''</math> w wyniku, którego otrzymamy w rzucie poziomym okrąg o promieniu '''r'''. Punkt <math>C''</math> zarysu przekroju zgodnie z wcześniejszymi analizami jest niewidoczny, pozostałe punkty należące do osi w rzucie pionowym są widoczne. W rzucie poziomym wszystkie punkty będą widoczne, ponieważ leżą powyżej płaszczyzny granicznej <math>\gamma''</math>. Wyznaczone w powyższy sposób rzuty osi pozwalają nam wykreślić zarys elipsy, będącej rzutem przekroju kuli. Punkty zmiany widoczności <math>K'</math> i <math>L'</math> w rzucie poziomym wyznaczymy na rzucie poziomym głównego południka kuli. W rzucie pionowym punkty te <math>K''</math> i <math>L''</math> leżą w miejscu przecięcia się płaszczyzny <math>\alpha''</math> z płaszczyzną <math>\gamma''</math> określającą granicę widoczności. | ||
| Linia 91: | Linia 91: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:CWGI_M5_Slajd9.png]] | ||
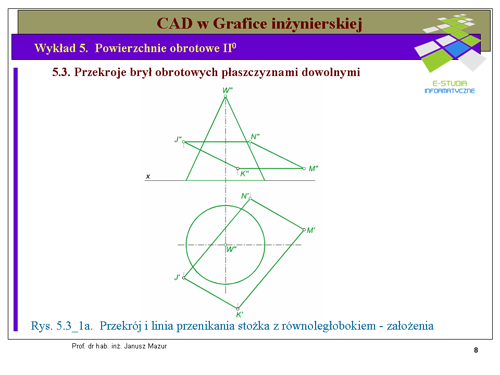
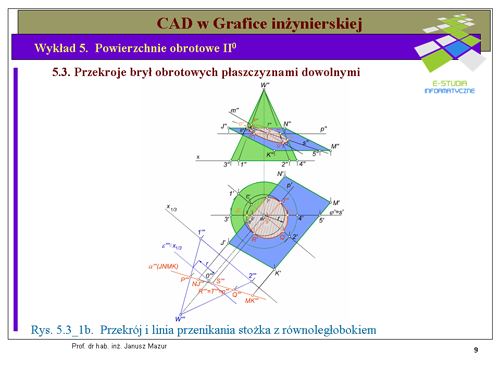
|valign="top"|Rozwiązanie zadania rozpoczynamy od zmiany układu odniesienia za pomocą transformacji tak, aby płaszczyzna krojąca była prostopadłą do rzutni (rys.5.3_1b). Ponieważ boki <math>JN</math> i <math>KM</math> równoległoboku są równoległe do rzutni poziomej (są prostymi poziomymi) oś transformacji | |valign="top"|Rozwiązanie zadania rozpoczynamy od zmiany układu odniesienia za pomocą transformacji tak, aby płaszczyzna krojąca była prostopadłą do rzutni (rys.5.3_1b). Ponieważ boki <math>JN</math> i <math>KM</math> równoległoboku są równoległe do rzutni poziomej (są prostymi poziomymi) oś transformacji <math>x_{1/3}</math> obieramy prostopadle do rzutów poziomych <math>J'N'</math> oraz <math>K'M'</math> boków równoległoboku. Po dokonaniu transformacji otrzymamy trzeci rzut stożka oraz trzeci rzut płaszczyzny równoległoboku <math>\alpha'''(JNMK)</math>. Przekrojem stożka, w tym przypadku jest elipsa (płaszczyzna <math>\alpha\ </math>, nie kroi podstawy). W trzecim rzucie wyznaczymy bez trudu dwie osie prostopadłe elipsy <math>P'''Q'''</math> oraz <math>R'''T'''</math>, które jednoznacznie opisują jej zarys. Wracając do układu rzutów poziomego i pionowego, zgodnie z zasadami transformacji, otrzymamy rzuty poziome i pionowe tych osi, które będą tworzyły średnice sprzężone elips odpowiednio dla rzutów poziomego i pionowego. Średnice sprzężone elips również jednoznacznie określają zarys elipsy. Kolejnym zagadnieniem do rozwiązania jest ustalenie punktów styczności elipsy w rzucie pionowym z tworzącymi konturowymi stożka, zwanymi '''punktami zmiany widoczności'''. W tym celu ustalamy granice zmiany widoczności dla rzutu pionowego stożka. Jest to płaszczyzna przechodząca przez wierzchołek, prostopadła do rzutni poziomej i równoległa do rzutni pionowej, której rzut poziomy opiszemy literą <math>\phi'</math>. Prowadząc przez tą płaszczyznę prostą <math>s\ </math>, leżącą w płaszczyźnie równoległoboku, możemy stwierdzić, iż będzie ona przechodziła również przez punkty zmiany widoczności, leżące na tworzących skrajnych w rzucie poziomym. Rzut pionowy prostej <math>s''</math> znajdziemy na rzucie pionowym równoległoboku <math>J''N''M''K''</math> wyznaczając kolejno rzuty punktów <math>5''</math> i <math>6''</math> należących do niej. Rzut pionowy prostej <math>s''</math> na tworzących skrajnych stożka w rzucie pionowym wyznaczy nam punkty zmiany widoczności <math>D''</math> i <math>C''</math>. Część elipsy przechodzącej przez punkty <math>R''D''C''</math> jest widoczna pozostała cześć elipsy jest niewidoczna. | ||
Aktualna wersja na dzień 12:01, 5 wrz 2023

|
Powierzchnie obrotowe |