Matematyka dyskretna 1/Wykład 8: Funkcje tworzące w zliczaniu obiektów kombinatorycznych

Obiekty kombinatoryczne często są zadane w sposób rekurencyjny. Tak zadawaliśmy np. drzewa binarne. Nawet, gdy obiekty nie są zadane w sposób rekurencyjny, to ich liczba (uzależniona np. od rozmiaru lub innego parametru) spełnia pewne zależności rekurencyjne. Często rozwikłanie takich zależności i wyprowadzenie wzoru na postać zwartą jest skomplikowane. W tym wykładzie zobaczymy jak w wielu przypadkach funkcje tworzące mogą być pomocne w zliczaniu różnych obiektów kombinatorycznych.

Zliczanie drzew

Drzewo binarne to dowolny obiekt powstały zgodnie z regułami:

• $\perp$ jest drzewem binarnym,

• jeśli $T_0$ i $T_1$ są drzewami binarnymi to $T_0\wedge T_1$ też jest drzewem binarnym.

Węzeł wewnętrzny drzewa binarnego jest zdefiniowany rekurencyjnie:

• drzewo $\perp$ nie ma węzłów wewnętrznych,

• węzłami wewnętrznymi drzewa $T_0\wedge T_1$ są wszystkie węzły wewnętrzne drzew $T_0$ i $T_1$ a także nowy węzeł łączący drzewa $T_0$ i $T_1$.

Liczba Catalana $c_n$ to liczba drzew binarnych o $n$ węzłach wewnętrznych.

Plik:Genfunc catalan.mp4

Wszystkie pełne drzewa binarne o 3 węzłach wewnętrznych

Drzewo T posiadające lewe poddrzewo T_l oraz prawe poddrzewo Tr

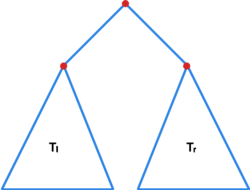
Przykład

Drzewa binarne są modelem dla tzw. wyrażeń nawiasowych, czyli termów z jednym działaniem binarnym i jedną zmienną $x$. Wyrażenia takie są zdefiniowane poprzez:

• zmienna $x$ jest wyrażeniem nawiasowym,

• jeśli $t_0$ i $t_1$ są wyrażeniami nawiasowymi, to $(t_0{t}_1)$ też jest wyrażeniem nawiasowym.

Węzły wewnętrzne wyrażenia nawiasowego, to podtermy nie będące zmiennymi.

Obserwacja 8.1

Liczby Catalana $c_n$ spełniają zależność rekurencyjną:

$\{\begin{array}{rcl}{c}_0& =& 1,\\ c_n& =& c_0{c}_{n-1}+c_1{c}_{n-2}+\dots +c_{n-1}{c}_0,\text{dla}n\ge 1.\end{array}$

Dowód

Pojedynczy wierzchołek jest jedynym pełnym drzewem binarnym bez węzłów wewnętrznych, a więc $c_0=1$. Każde drzewo o co najmniej jednym wierzchołku wewnętrznym rozkłada się jako $T_l\wedge T_r$, dla pewnych jednoznacznie wyznaczonych poddrzew $T_l,T_r$. Poddrzewo $T_l$ nazywamy lewym, a $T_r$ prawym podrzewem drzewa $T_l\wedge T_r$.

Niech teraz

• $T_n$ będzie rodziną wszystkich drzew binarnych o $n$ węzłach wewnętrznych, oraz

• $T_{n_l,n_r}$ będzie rodziną wszystkich drzew, których lewe i prawe poddrzewo mają odpowiednio $n_l$ oraz $n_r$ węzłów wewnętrznych.

Zachodzi więc:

$\left|T_{n_l,n_r}\right|=|T_{n_l}\times T_{n_r}|=\left|T_{n_l}\right|\cdot \left|T_{n_r}\right|=c_{n_l}\cdot c_{n_r}$

Ponadto, jeśli drzewo o $n$ wierzchołkach wewnętrznych posiada lewe poddrzewo o $n_l$ wierzchołkach wewnętrznych oraz prawe poddrzewo o $n_r$ węzłów wewnętrznych to $n=n_l+n_r+1$. Zatem rodzina wszystkich drzew o $n$ wewnętrznych wierzchołkach rozbija się na rozłączną sumę

$T_n=T_{0,n-1}\cup T_{1,n-2}\cup \dots \cup T_{n-1,0}$

W konsekwencji otrzymujemy:

$c_n=c_0{c}_{n-1}+c_1{c}_{n-2}+\dots +c_{n-1}{c}_0$

Wniosek 8.2

Funkcja tworząca $C(x)=c_0+c_{1}x+c_2{x}^2+\dots$ dla ciągu liczb Catalana spełnia

$C(x)=\frac{1-\sqrt{1-4x}}{2x}$

Dowód

Używając zależności rekurencyjnej z Obserwacji 8.1 otrzymujemy:

$\begin{array}{rl}C(x)& =\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n\\ & =1+\sum _{n=1}^{\mathrm{\infty }}(c_0{c}_{n-1}+c_1{c}_{n-2}+\dots +c_{n-1}{c}_0)x^n\\ & =1+xC(x)C(x)\end{array}$

skąd natychmiast:

$C(x)=\frac{1\pm \sqrt{1-4x}}{2x}$

Warunek $C(0)=c_0=1$ eliminuje rozwiązanie $C(x)\cdot 2x=1+\sqrt{1-4x}$, a zatem

$C(x)=\frac{1-\sqrt{1-4x}}{2x}$

Twierdzenie 8.3

Liczby Catalana wyrażają się wzorem

$c_n=\frac{1}{n+1}(\genfrac{}{}{0ex}{}{2n}{n})$

Dowód

Twierdzenie o rozwinięciu funkcji $(1+x{)}^y$ w szereg daje

$\sqrt{1-4x}=\sum _{n=0}^{\mathrm{\infty }}(\genfrac{}{}{0ex}{}{1/2}{n}){(-4x)}^n$.

Podstawiając powyższe rozwinięcie $\sqrt{1-4x}$ do wzoru na $C(x)$ otrzymanego we Wniosku 8.2 po dokonaniu kilku prostych przekształceń otrzymujemy:

$C(x)=\frac{1-\sqrt{1-4x}}{2x}=\sum _{n=0}^{\mathrm{\infty }}\frac{(1-1/2)\cdot \dots \cdot (n-1/2)}{(n+1)!}{4}^n{x}^n$

czyli

$c_n=\frac{(1-1/2)\cdot \dots \cdot (n-1/2)}{(n+1)!}{4}^n$

Iloczyn $(1-1/2)\cdot \dots \cdot (n-1/2)$ po wymnożeniu przez $2^n$ przyjmuje postać

$\prod _{k=1}^n(2k-1)=1\cdot 3\cdot \dots \cdot (2n-3)\cdot (2n-1)$

Mnożąc więc teraz ten iloczyn $2^{n}n!$ otrzymujemy:

$2^{n}n!\prod _{k=1}^n(2k-1)=1\cdot 2\cdot 3\cdot \dots \cdot (2n-2)\cdot (2n-1)\cdot 2n=\left(2n\right)!$

Tym samym dostajemy

$c_n=\frac{1}{n+1}(\genfrac{}{}{0ex}{}{2n}{n})$

Używając ostatniego Twierdzenia, można określic asymptotyczne zachowanie liczb Catalana.

Wniosek 8.4

Asymptotyczne zachowanie liczb Catalana dane jest przez

$c_n\sim \frac{4^{n+1}}{4(n+1)\sqrt{\pi n}}$

tzn.

$\underset{n\mapsto \mathrm{\infty }}{\lim }\frac{c_n\cdot 4^{n+1}}{4(n+1)\sqrt{\pi n}}=1$

W praktyce często pojawia się konieczność zliczania drzew z uwagi na ich wysokość. Odpowiada to zliczaniu termów z uwagi na zagłębienie.

Wysokość drzewa określona jest rekurencyjnie jako:

• $\mathsf{h}(\perp )=0$,

• $\mathsf{h}(T_0\wedge T_1)=\max (\mathsf{h}(T_0),\mathsf{h}(T_1))+1$.

Obserwacja 8.5

Liczba $t_h$ drzew binarnych o wysokości co najwyżej $h$ wyraża się równaniem rekurencyjnym

$\{\begin{array}{rcl}{t}_0& =& 1,\\ t_h& =& t_{h-1}^2+1\text{dla}h>1.\end{array}$

Dowód

Niech $T_h$ będzie rodziną pełnych drzew binarnych o wysokości co najwyżej $h$. Wtedy $t_h=\left|T_h\right|$. Oczywiście $T_0=\{\perp \}$, a więc $t_0=1$. Jedynym drzewem w $T_h$, które nie jest rozkładalne na lewe i prawe poddrzewo jest drzewo $\perp$. Każde więc drzewo $T_0\in T_h-\{\perp \}$ jest postaci $T_0=T_l\wedge T_r$, gdzie poddrzewa $T_l$ oraz $T_r$ są wysokości co najwyżej $h-1$, tzn. $T_l,T_r\in T_{h-1}$. Dowolne więc drzewo z $T_h$ wyznacza jednoznacznie parę drzew z $T_{h-1}$. Odwzorowanie to jest bijekcją, więc

$\left|T_h\right|=\left|T_{h-1}\right|\cdot \left|T_{h-1}\right|+1$,

skąd natychmiast dostajemy naszą zależność rekurencyjną.

Plik:Zliczanie drzewa wys.svg

Drzewa o wysokości co najwyżej 2

Wniosek 8.6

Dla $h\ge 1$ mamy:

$2^{2^{h-1}}\le t_h\le 2^{2^h-1}$,

Dowód

Dowód przeprowadzimy indukcyjnie ze względu na $h$. Dla $h=1$ mamy $t_1=t_0^2+1=2$, oraz $2^{2^{h-1}}=2=2^{2^h-1}$ Niech więc $h>1$ i załóżmy dla indukcji, że

$2^{2^{h-2}}\le t_{h-1}\le 2^{2^{h-1}-1}$

Wtedy:

${\left(2^{2^{h-2}}\right)}^2+1\le t_{h-1}^2+1\le {\left(2^{2^{h-1}-1}\right)}^2+1$

skąd natychmiast:

$2^{2^{h-1}}\le {\left(2^{2^{h-2}}\right)}^2+1\le t_h\le {\left(2^{2^{h-1}-1}\right)}^2+1=2^{2^h-2}+1=\frac{1}{4}{2}^{2^h}+1\le 2^{2^h-1}$

Zliczanie podziałów liczby na sumy

Przypomnijmy, że przez $P(n,k)$ oznaczyliśmy liczbę podziałów liczby $n$ na dokładnie $k$ składników. Wtedy $p_n=\sum _{k=1}^{n}P(n,k)$ oznacza liczbę wszystkich możliwych podziałów liczby $n$ na sumę.

Przykład

Policzmy wszystkie sposoby przedstawienia liczby $6$ za pomocą sumy dodatnich liczb naturalnych.

$6=a_0+a_1+\dots +a_{k-1}$,

gdzie $k$ oraz $a_0\le a_1\le \dots \le a_{k-1}$ są dodatnimi liczbami naturalnymi. Oto one

$\begin{array}{rclcrcl}6& =& 1+1+1+1+1+1& & 6& =& 2+2+2\\ 6& =& 1+1+1+1+2& & 6& =& 1+5\\ 6& =& 1+1+1+3& & 6& =& 2+4\\ 6& =& 1+1+2+2& & 6& =& 3+3\\ 6& =& 1+1+4& & 6& =& 6\\ 6& =& 1+2+3& & & & \end{array}$

tzn. $p_6=11$.

Funkcja tworząca podziału liczby na sumy to szereg

$P(x)=p_0+p_{1}x+p_2{x}^2+p_3{x}^3+\dots$

Ponadto funkcja tworząca podziału liczby na sumy złożone wyłącznie z liczb $k_1,k_2,\dots ,k_m$ oznaczać będziemy przez

$P_{k_1,k_2,\dots ,k_m}(x)=p{\text{'}}_0+p{\text{'}}_{1}x+p{\text{'}}_2{x}^2+p{\text{'}}_3{x}^3+\dots$,

gdzie $p{\text{'}}_n$ to liczba podziałów liczby $n$ na sumę $n=a_0+a_1+\dots +a_{k-1}$, gdzie $k\in \mathbb{\mathbb{N}}-\left\{0\right\}$ oraz $a_0,a_1,\dots ,a_{k-1}\in \left\{k_1,k_2,\dots ,k_m\right\}$.

Przykład

Pierwszy przykład w wykładzie o funkcjach tworzących dotyczył możliwości rozmiany kwoty za pomocą jednocentówek, pięciocentówek, dziesięciocentówek, ćwierćdolarówek oraz półdolarówek. Rozważaliśmy więc tam funkcję tworzącą $P_{1,5,10,25,50}(x)$.

Obserwacja 8.7

$P_k(x)=1+x^k+x^{2k}+x^{3k}+\dots =\frac{1}{1-x^k}$

Dowód

Niech $p_{k,n}$ będzie liczbą rozkładów liczby $n$ na sumę złożoną wyłącznie ze składników równych $k$. Oczywiście jeśli $k$ dzieli $n$, to istnieje dokładnie jedna suma $n=k+k+\dots +k$. Jeśli natomiast $n$ nie jest podzielne przez $k$, to taki rozkład nie istnieje, tak więc

$p_{k,n}=\{\begin{array}{ll}1,& \text{jeśli}n=ak\text{dla}a=0,1,2,\dots \\ 0,& \text{w przeciwnym wypadku.}\end{array}$

Otrzymujemy w ten sposób

$\begin{array}{rl}{P}_k(x)& =p_{k,0}+p_{k,1}x+p_{k,2}{x}^2+\dots \\ & =1+x^k+x^{2k}+x^{3k}+\dots ,\end{array}$

która to funkcja zwija się do

$P_k(x)=\frac{1}{1-x^k}$

Obserwacja 8.8

$P_{k_1,k_2,\dots ,k_m}(x)=P_{k_1}(x)\cdot P_{k_2}(x)\cdot \dots \cdot P_{k_m}(x)=\frac{1}{1-x^{k_1}}\cdot \frac{1}{1-x^{k_2}}\cdot \dots \cdot \frac{1}{1-x^{k_m}}$.

Dowód

Załóżmy, że splot

$(1+x^{k_1}+x^{2k_1}+\dots )\cdot (1+x^{k_2}+x^{2k_2}+\dots )\cdot \cdot (1+x^{k_m}+x^{2k_m}+\dots )$

jest przedstawiony jako szereg $p{\text{'}}_0+p{\text{'}}_{1}x+p{\text{'}}_2{x}^2+p{\text{'}}_3{x}^3+\dots$. Wtedy oczywiście $p{\text{'}}_n{x}^n$ jest sumą wszystkich jednomianów postaci $x^{j_1{k}_{l_1}}\cdot x^{j_2{k}_{l_2}}\cdot \dots \cdot x^{j_s{k}_{l_s}}$, dla których $x^n=x^{j_1{k}_{l_1}}\cdot x^{j_2{k}_{l_2}}\cdot \dots \cdot x^{j_s{k}_{l_s}}$. Współczynnik $p{\text{'}}_n$ więc jest liczbą wszystkich ciągów $s,j_1,\dots ,j_s,l_1,\dots ,l_s$ takich, że

$\begin{array}{rl}n& =j_1{k}_{l_1}+j_2{k}_{l_2}+\dots +j_s{k}_{l_s}\\ & =(k_{l_1}+\dots +k_{l_1})+(k_{l_2}+\dots +k_{l_2})+\dots +(k_{l_s}+\dots +k_{l_s}),\end{array}$

tzn. $p{\text{'}}_n$ jest liczbą rozkładów liczby $n$ na sumy o składnikach ze zbioru $\left\{k_1,k_2,\dots ,k_n\right\}$, a zatem $p{\text{'}}_n$ jest $n$-tym współczynnikiem funkcji tworzącej $P_{k_1,k_2,\dots ,k_m}(x)$.

Przykład

Niech $P_{1,2,3,4}(x)=p^{\prime }{\text{'}}_0+p^{\prime }{\text{'}}_{1}x+p^{\prime }{\text{'}}_2{x}^2+\dots$. Współczynnik $p^{\prime }{\text{'}}_6$ to liczba iloczynów postaci $x^{j_1{k}_{l_1}}\cdot x^{j_2{k}_{l_2}}\cdot \dots \cdot x^{j_s{k}_{l_s}}$ równych $x^6$, a zarazem liczba podziałów liczby $6$ na sumy złożone ze składników $1,2,3$ oraz $4$. Każdemu iloczynowi odpowiada jeden podział. Na przykład $x^{1\cdot 4}\cdot x^{2\cdot 1}$, gdzie $x^{1\cdot 4}$ pochodzi z $P_1(x)$ oraz $x^{2\cdot 1}$ pochodzi z $P_2(x)$, odpowiada sumie $6=1+1+1+1+2$. Poniżej zaznaczono w funkcji tworzącej $P_{1,2,3,4}(x)$ jednomiany ${\mathbf{𝐱}}^{(\mathrm{𝟏}+\mathrm{𝟏}+\mathrm{𝟏}+\mathrm{𝟏})}$ oraz ${\mathbf{𝐱}}^{\mathbf{𝟐}}$

$\begin{array}{l}{P}_{1,2,3,4}(x)=1+x+2x^2+3x^3+4x^4+6x^5+7x^6+\dots \\ =(1+x^1+x^{(1+1)}+x^{(1+1+1)}+{\mathbf{𝐱}}^{(\mathrm{𝟏}+\mathrm{𝟏}+\mathrm{𝟏}+\mathrm{𝟏})}+x^{(1+1+1+1+1)}+x^{(1+1+1+1+1+1)}+\dots )\\ =\cdot (1+{\mathbf{𝐱}}^{\mathbf{𝟐}}+x^{(2+2)}+x^{(2+2+2)}+x^{(2+2+2+2)}+x^{(2+2+2+2+2)}+\dots )\\ =\cdot (1+x^3+x^{(3+3)}+x^{(3+3+3)}+x^{(3+3+3+3)}+x^{(3+3+3+3+3)}+\dots )\\ =\cdot (1+x^4+x^{(4+4)}+x^{(4+4+4)}+x^{(4+4+4+4)}+x^{(4+4+4+4+4)}+\dots )\end{array}$

Odpowiadają one zaznaczonemu rozkładowi na liście wszystkich rozkładów liczby $6$:

$\begin{array}{lcl}6=1+1+1+1+1+1,& & 6=1+2+3,\\ \underset{\_}{\mathbf{6}\mathbf{=}\mathbf{1}\mathbf{+}\mathbf{1}\mathbf{+}\mathbf{1}\mathbf{+}\mathbf{1}\mathbf{+}\mathbf{2}},& & 6=2+2+2,\\ 6=1+1+1+3,& & 6=3+3.\\ 6=1+1+2+2,& & \end{array}$

Przykład

W funkcji tworzącej

$P_{1,5,10,25,50}(x)=p^{″}{\text{'}}_0+p^{″}{\text{'}}_{1}x+p^{″}{\text{'}}_2{x}^2+\dots$

współczynnik $p^{″}{\text{'}}_n$ jest liczbą podziałów liczby $n$ na sumy postaci

$n=1+\dots +1+5+\dots +5+10+\dots +10+25+\dots +25+50+\dots +50$,

czyli liczbą sposobów na jakie można rozmienić $n$ centów przy użyciu jednocentówek, pięciocentówek, dziesięciocentówek, ćwierćdolarówek oraz półdolarówek. Otrzymaliśmy więc rozwiązanie przykładu o rozmienianiu monet. Funkcja tworząca jest w poznanej już postaci równej

$P_{1,5,10,25,50}(x)=\frac{1}{1-x}\cdot \frac{1}{1-x^5}\cdot \frac{1}{1-x^{10}}\cdot \frac{1}{1-x^{25}}\cdot \frac{1}{1-x^{50}}$

Widzieliśmy już, że ogólnie

$P_{k_1{k}_2\dots k_m}(x)=\frac{1}{1-x^{k_1}}\cdot \frac{1}{1-x^{k_2}}\cdot \dots \cdot \frac{1}{1-x^{k_m}}$

Twierdzenie 8.9[L. Euler]

Funkcja tworząca podziału liczby na sumy jest przedstawialna jako

$P(x)=\prod _{k=1}^{\mathrm{\infty }}\frac{1}{1-x^k}=\frac{1}{1-x}\cdot \frac{1}{1-x^2}\cdot \dots \cdot \frac{1}{1-x^n}\cdot \dots$

Dowód

Niech $P_{\left(m\right)}(x)=P_{1,2,\dots ,m}(x)$ rozwija się w szereg $\sum _{n=0}^{\mathrm{\infty }}{p}_{\left(m\right)n}{x}^n$, a formalny nieskończony splot

$\prod _{k=1}^{\mathrm{\infty }}{P}_k(x)=\prod _{k=1}^{\mathrm{\infty }}\frac{1}{1-x^k}=\prod _{k=1}^{\mathrm{\infty }}(1+x^k+x^{2k}+x^{3k}+\dots )$

zwija się do szeregu formalnego

$F(x)=f_0+f_{1}x+f_2{x}^2+f_3{x}^3+\dots$

Oczywiście przy liczeniu $f_n$ z czynników $(1+x^k+x^{2k}+x^{3k}+\dots )$, gdzie $k>n$, jedynie jednomian $1$ odgrywa rolę, gdyż jednomiany $x^{lk}$ z $l\ge 1$ dają zbyt duże potęgi. A zatem $f_n=p_{\left(n\right)n}$. Ponieważ żaden składnik w rozkładzie $n=a_0+a_1+\dots +a_s$ nie może przekraczać $n$, mamy $p_n=p_{\left(n\right)n}$, skąd natychmiast $f_n=p_n$, co kończy dowód.

Funkcje tworzące dla liczb Stirlinga oraz liczb Bella

Twierdzenie 8.10

Funkcja tworząca

$s_n(x)=\left[\begin{array}{c}n\\ 0\end{array}\right]+\left[\begin{array}{c}n\\ 1\end{array}\right]x+\left[\begin{array}{c}n\\ 2\end{array}\right]x^2+\left[\begin{array}{c}n\\ 3\end{array}\right]x^3+\dots$,

dla cyklowych liczb Stirlinga $\left[\begin{array}{c}n\\ m\end{array}\right]$ ma postać zwartą

$s_n(x)=x^{\bar{n}}=x\cdot (x+1)\cdot (x+n-1)$

Dowód

Cyklowe liczby Stirlinga spełniają następującą zależność rekurencyjną

$\begin{array}{rcll}\left[\begin{array}{c}n\\ 0\end{array}\right]& =& 0,& \text{dla}n>0,\\ \left[\begin{array}{c}n\\ k\end{array}\right]& =& 0,& \text{dla}k<n,\\ \left[\begin{array}{c}k\\ k\end{array}\right]& =& 1,& \text{dla}k\ge 0,\\ \left[\begin{array}{c}n\\ k\end{array}\right]& =& (n-1)\left[\begin{array}{c}n-1\\ k\end{array}\right]+\left[\begin{array}{c}n-1\\ k-1\end{array}\right],& \text{dla}0>k>n.\end{array}$

Po podstawieniu tych zależności w rozwinięciu funkcji tworzącej $s_k(x)$ otrzymujemy

$s_n(x)=(n-1)s_{n-1}(x)+x{s}_{n-1}(x)=(x+n-1)s_{n-1}(x)$

Iterując powyższą równość otrzymujemy:

$s_{n}x=(z+n-1)\cdot (z+n-2)\cdot \dots \cdot (x+1)\cdot x=x^{\bar{n}}$,

co kończy dowód.

Twierdzenie 8.11

Funkcja tworząca

$S_k(x)=\left\{\begin{array}{c}k\\ k\end{array}\right\}+\left\{\begin{array}{c}k+1\\ k\end{array}\right\}x+\left\{\begin{array}{c}k+2\\ k\end{array}\right\}{x}^2+\left\{\begin{array}{c}k+3\\ k\end{array}\right\}{x}^3+\dots$

dla podziałowych liczb Stirlinga $\left\{\begin{array}{c}n\\ m\end{array}\right\}$ ma postać zwartą

$S_k(x)=\frac{1}{(1-x)\cdot (1-2x)\cdot \dots \cdot (1-kx)}$

Dowód

Podziałowe liczby Stirlinga spełniają następującą zależność rekurencyjną

$\begin{array}{rcll}\left\{\begin{array}{c}n\\ 0\end{array}\right\}& =& 0,& \text{dla}n>0,\\ \left\{\begin{array}{c}k\\ k\end{array}\right\}& =& 1,& \text{dla}k\ge 0,\\ \left\{\begin{array}{c}n+k\\ k\end{array}\right\}& =& k\left\{\begin{array}{c}n+k-1\\ k\end{array}\right\}+\left\{\begin{array}{c}n+k-1\\ k-1\end{array}\right\},& \text{dla}n>1,k>0.\end{array}$

Po podstawieniu tych zależności w rozwinięciu funkcji tworzącej $S_k(x)$ otrzymujemy:

$S_k(x)=kx{S}_k(x)+S_{k-1}(x)$,

skąd natychmiast:

$S_k(x)=\frac{1}{1-kx}{S}_{k-1}(x)$

Iterując powyższą równość otrzymujemy:

$S_k(x)=\frac{1}{(1-kx)\cdot (1-(k-1)x)\cdot \dots \cdot (1-x)}$,

co kończy dowód.

Czasem, dla liczenia współczynników funkcji tworzącej wygodnie użyć jest rachunku różniczkowego i rozwinięcia funkcji w szereg Taylora. Dlatego dla ciągu $(g_0,g_1,g_2,g_3,\dots )$ obok funkcji tworzącej

$G(x)=\sum _{n=0}^{\mathrm{\infty }}{g}_n{x}^n=g_0+g_{1}x+g_2{x}^2+g_3{x}^3+g_4{x}^4+\dots$

rozważa się też tzw. wykładniczą funkcję tworzącą, tzn. wyrażenie postaci

$\sum _{n=0}^{\mathrm{\infty }}\frac{g_n}{n!}{x}^n=\frac{g_0}{0!}+\frac{g_1}{1!}x+\frac{g_2}{2!}{x}^2+\frac{g_3}{3!}{x}^3+\frac{g_4}{4!}{x}^4+\dots$

Twierdzenie 8.12

Wykładnicza funkcja tworząca

$B(x)=\sum _{n=0}^{\mathrm{\infty }}\frac{B_n}{n!}{x}^n=\frac{B_0}{0!}+\frac{B_1}{1!}x+\frac{B_2}{2!}{x}^2+\frac{B_3}{3!}{x}^3+\dots$

dla liczb Bell'a $B_0,B_1,B_2,B_3,\dots$ ma postać zwartą

$B(x)=e^{(e^x-1)}$

Dowód

Liczby Bella spełniają następującą zależność rekurencyjną

$\begin{array}{rcl}{B}_0& =& 1,\\ B_{n+1}& =& (\genfrac{}{}{0ex}{}{n}{0})B_0+(\genfrac{}{}{0ex}{}{n}{1})B_1+(\genfrac{}{}{0ex}{}{n}{2})B_2+\dots +(\genfrac{}{}{0ex}{}{n}{n})B_n,\text{dla}n>0.\end{array}$

Pochodna szeregu $B(x)=\sum _{n=0}^{\mathrm{\infty }}\frac{B_n}{n!}{x}^n$ to

$B^{\prime }(x)=\sum _{n=1}^{\mathrm{\infty }}\frac{n{B}_n}{n!}{x}^{n-1}=\sum _{n=0}^{\mathrm{\infty }}\frac{B_n}{n!}{x}^n$

Dzieląc obustronnie przez $n!$ zależność rekurencyjną dla liczb Bella otrzymujemy

$\frac{1}{n!}\cdot B_{n+1}=\frac{1}{0!}\cdot \frac{1}{n!}\cdot B_0+\frac{1}{1!}\cdot \frac{1}{(n-1)!}\cdot B_1+\dots +\frac{1}{n!}\cdot \frac{1}{0!}\cdot B_n$

Prawa strona tej równości jest współczynnikiem przy $x^n$ splotu funkcji $e^x$ z $B(x)$. Otrzymujemy więc równość

$B^{\prime }(x)=e^{x}B(x)$,      (2)

której rozwiązaniem przyjmującym wartość $B(0)=B_0=1$ jest

$B(x)=e^{(e^x-1)}$

Faktycznie, po podstawieniu rozwiązania do równości (2) uzyskujemy:

$B^{\prime }(x)=(e^{(e^x-1)}{)}^{\prime }=e^x{e}^{(e^x-1)}=e^{x}B(x)$.