GKIW Moduł 5 - Reprezentacja przestrzeni trójwymiarowej na płaszczyźnie: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 18: | Linia 18: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M5_Slajd1_v4.png|thumb|500px]] | ||
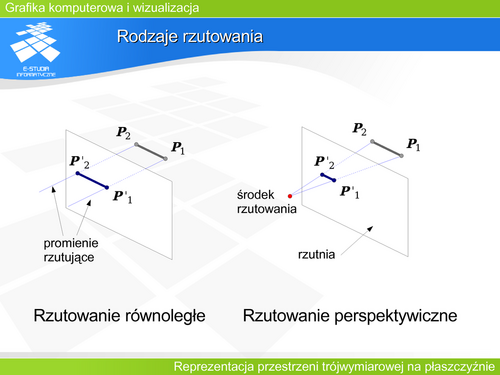
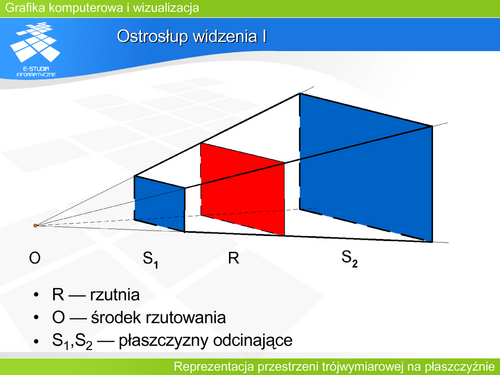
|valign="top"|Rzutowanie jest przekształceniem przestrzeni trójwymiarowej na przestrzeń dwuwymiarową. Rzutowanie polega na poprowadzeniu prostej przez dany punkt obiektu i znalezieniu punktu wspólnego tej prostej z rzutnią. Wyznaczony punkt nazywany jest rzutem a prosta promieniem rzutującym. | |valign="top"|Rzutowanie jest przekształceniem przestrzeni trójwymiarowej na przestrzeń dwuwymiarową. Rzutowanie polega na poprowadzeniu prostej przez dany punkt obiektu i znalezieniu punktu wspólnego tej prostej z rzutnią. Wyznaczony punkt nazywany jest rzutem a prosta promieniem rzutującym. | ||
| Linia 79: | Linia 79: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M5_Slajd6_v4.png|thumb|500px]] | ||
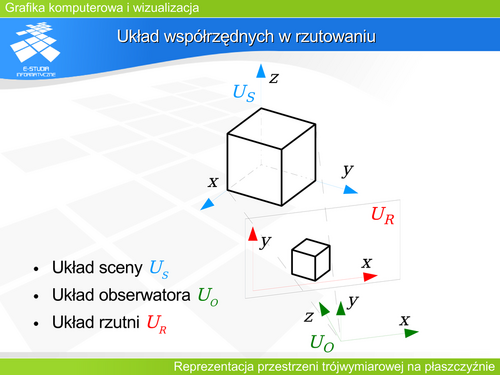
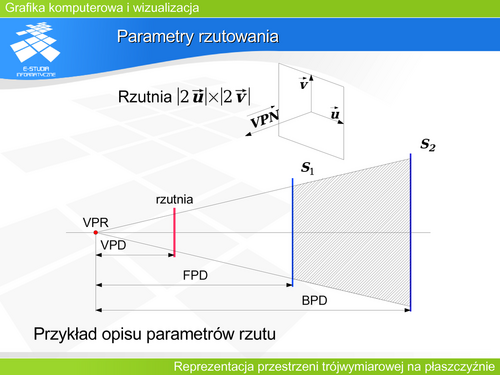
|valign="top"|Rzutowanie jest realizowane w układzie obserwatora (lewoskrętnym). | |valign="top"|Rzutowanie jest realizowane w układzie obserwatora (lewoskrętnym). | ||
| Linia 177: | Linia 177: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M5_Slajd15_v4.png|thumb|500px]] | ||
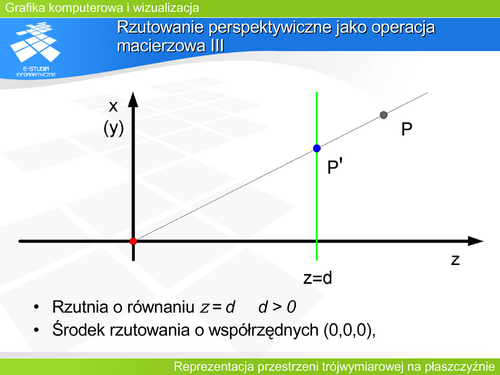
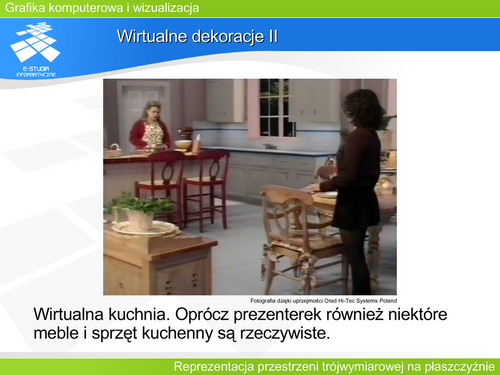
|valign="top"|Patrząc na rzutowanie poprzez analogię do aparatu fotograficznego warto zwrócić uwagę na parametry decydujące o obrazie, który powstanie. Fotograf, wybierając temat do zdjęcia, określa położenie aparatu i kierunek fotografowania. Określa także ogniskową obiektywu (funkcja zoom) czyli kąt „widzenia” aparatu. Warto przy tym pamiętać, że zdjęcie wykonane obiektywem szerokokątnym z bliskiej odległości jest inne niż obiektywem wąskokątnym (teleobiektywem) z dużej odległości, pomimo pozornego podobieństwa wybranych fragmentów. Dobranie właściwego ostrosłupa widzenia jest szczególnie istotne w grach komputerowych i zastosowaniach filmowych grafiki komputerowej. Przekładając parametry ruchu aparatu (fotografa) na parametry rzutowania definiujemy '''wirtualną kamerę'''. Jaki jest minimalny zestaw operacji, zapewniający pełną swobodę manipulacji taką kamerą? | |valign="top"|Patrząc na rzutowanie poprzez analogię do aparatu fotograficznego warto zwrócić uwagę na parametry decydujące o obrazie, który powstanie. Fotograf, wybierając temat do zdjęcia, określa położenie aparatu i kierunek fotografowania. Określa także ogniskową obiektywu (funkcja zoom) czyli kąt „widzenia” aparatu. Warto przy tym pamiętać, że zdjęcie wykonane obiektywem szerokokątnym z bliskiej odległości jest inne niż obiektywem wąskokątnym (teleobiektywem) z dużej odległości, pomimo pozornego podobieństwa wybranych fragmentów. Dobranie właściwego ostrosłupa widzenia jest szczególnie istotne w grach komputerowych i zastosowaniach filmowych grafiki komputerowej. Przekładając parametry ruchu aparatu (fotografa) na parametry rzutowania definiujemy '''wirtualną kamerę'''. Jaki jest minimalny zestaw operacji, zapewniający pełną swobodę manipulacji taką kamerą? | ||
Wersja z 22:46, 27 lis 2007
Wykład
 |
 |
 |
Warto zwrócić uwagę na to, że macierz definiuje operację wymagającą normalizacji. |
 |
W tym wariancie opisu rzutowania perspektywicznego macierz wynikowa również wymaga normalizacji.
Oba warianty definicji rzutowania perspektywicznego mogą być stosowane zamiennie zależnie od sytuacji. |
 |
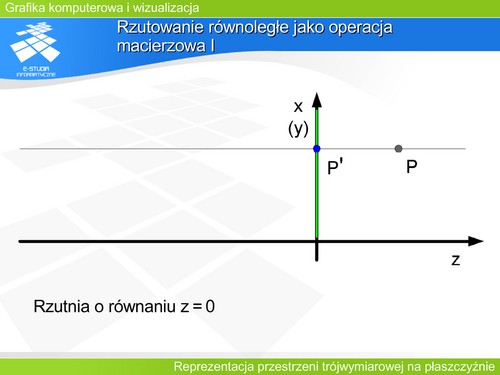
Macierz opisująca rzutowanie równoległe będzie miała następującą postać:
Operacja w tym przypadku nie wymaga normalizacji. |
Literatura
 |