|
|
| Linia 238: |
Linia 238: |
| |width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd32.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd32.png|thumb|500px]] |
| |valign="top"| | | |valign="top"| |
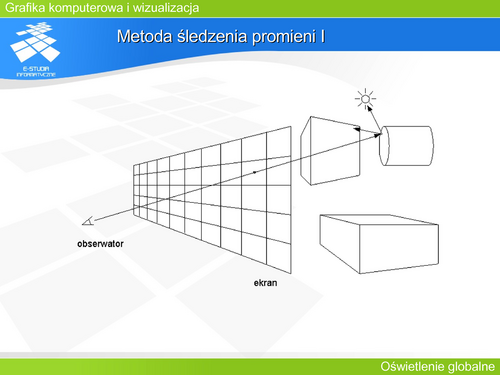
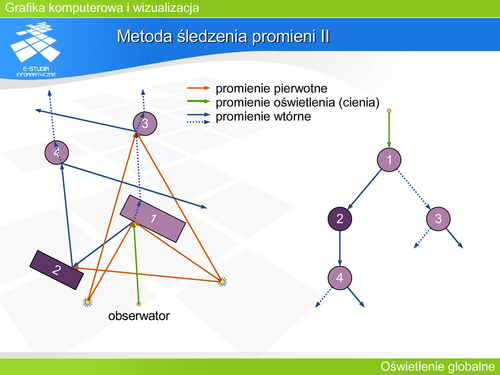
| Metoda śledzenia promieni III | | '''Metoda śledzenia promieni III''' |
|
| |
|
| Istnieje kilka różnych wersji realizacji tego algorytmu: | | Istnieje kilka różnych wersji realizacji tego algorytmu: |
| Linia 273: |
Linia 273: |
|
| |
|
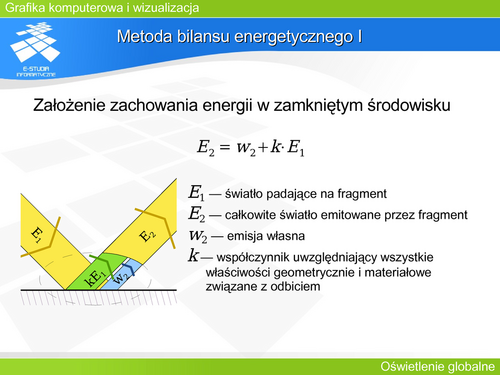
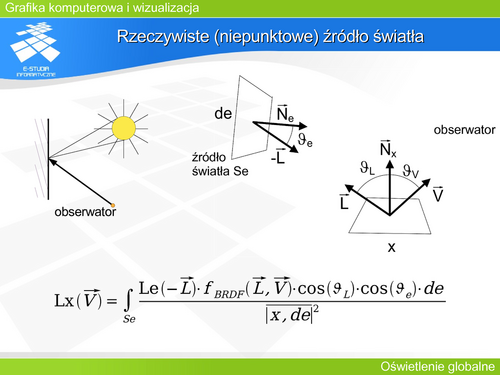
| Problem z opisem rzeczywistych obiektów za pomocą klasycznego śledzenia Whitteda zaczyna się pojawiać gdy weźmiemy pod uwagę rzeczywiste źródło światła (o skończonych – niepomijalnych rozmiarach). Analiza oświetlenia na drodze jednego promienia przestaje odpowiadać rzeczywistości. Osiągnięcie obrazu miękkiego półcienia jest całkowicie niemożliwe. | | Problem z opisem rzeczywistych obiektów za pomocą klasycznego śledzenia Whitteda zaczyna się pojawiać gdy weźmiemy pod uwagę rzeczywiste źródło światła (o skończonych – niepomijalnych rozmiarach). Analiza oświetlenia na drodze jednego promienia przestaje odpowiadać rzeczywistości. Osiągnięcie obrazu miękkiego półcienia jest całkowicie niemożliwe. |
| Rozpatrując fragment powierzchni oświetlony bezpośrednio przez źródło powierzchniowe i biorąc pod uwagę równanie wizualizacji Kajiya, można wykazać, że luminancja <math>LX(\breve{V} )</math> postrzegana na powierzchni <math>x</math> z kierunku wektora <math>\breve{V}</math> będzie opisana przedstawionym równaniem. Poprawny wynik może dać tylko analiza uwzględniająca całkowanie powierzchni źródła światła. | | Rozpatrując fragment powierzchni oświetlony bezpośrednio przez źródło powierzchniowe i biorąc pod uwagę równanie wizualizacji Kajiya, można wykazać, że luminancja <math>Lx(\breve{V} )</math> postrzegana na powierzchni <math>x</math> z kierunku wektora <math>\breve{V}</math> będzie opisana przedstawionym równaniem. Poprawny wynik może dać tylko analiza uwzględniająca całkowanie powierzchni źródła światła. |
| Przykładem dobrej aproksymacji przy wykorzystaniu klasycznej metody śledzenia jest model Verbecka i Greenberga z 1984 roku. Zakłada on, że źródło powierzchniowe jest przybliżone zbiorem źródeł punktowych rozłożonych na powierzchni źródła. | | Przykładem dobrej aproksymacji przy wykorzystaniu klasycznej metody śledzenia jest model Verbecka i Greenberga z 1984 roku. Zakłada on, że źródło powierzchniowe jest przybliżone zbiorem źródeł punktowych rozłożonych na powierzchni źródła. |
|
| |
|
| Linia 293: |
Linia 293: |
| to możemy skorzystać z N liczb losowych o rozkładzie równomiernym <math>x_1, x_2, ,,,x_N</math>, stanowiących pewną realizację zmiennej losowej <math>X</math>. Wtedy | | to możemy skorzystać z N liczb losowych o rozkładzie równomiernym <math>x_1, x_2, ,,,x_N</math>, stanowiących pewną realizację zmiennej losowej <math>X</math>. Wtedy |
| | | |
| <math>I \approx \frac{1}{N} \\sum_{i=1}^N h(x_i)</math> | | <math>I \approx \frac{1}{N} \sum_{i=1}^N h(x_i)</math> |
|
| |
|
| Oczywiście takie proste całkowanie nie byłoby przydatne, gdyż w praktyce problem zachodzi w pewnym przedziale <math>S</math> i jednocześnie wymagane jest losowanie próbek o rozkładzie innym niż równomierny. Podane wzory określają takie rozwiązanie. | | Oczywiście takie proste całkowanie nie byłoby przydatne, gdyż w praktyce problem zachodzi w pewnym przedziale <math>S</math> i jednocześnie wymagane jest losowanie próbek o rozkładzie innym niż równomierny. Podane wzory określają takie rozwiązanie. |