GKIW Moduł 7

---

---

Problem rozstrzygania widoczności Problem eliminacji elementów zasłoniętych (zwany także problemem rozstrzygania widoczności lub problemem wyznaczania powierzchni widocznych) polega na określeniu, które fragmenty obiektów sceny mogą być widoczne przez wirtualną kamerę (przez obserwatora). Problem wydaje się nam banalny, ale aby w wirtualnym świecie zaszło naturalne dla naszego widzenia zasłanianie jednych obiektów przez drugie, to trzeba to opisać odpowiednim algorytmem. Jest to przykład problemu, dla którego nie jest znane jedno, uniwersalne rozwiązanie. Generalnie rzecz biorąc, zadanie to można traktować jako szeroko rozumiany problem sortowania. Z punkt widzenia obserwatora obiekty leżące dalej są zasłonięte przez obiekty leżące bliżej. Niestety to proste stwierdzenie nie przekłada się na równie prosty algorytm. Już samo określenie „jeden obiekt leżący dalej od drugiego” może prowadzić do niejednoznaczności, gdyż trudno przypisać jedną miarę odległości obiektowi zajmującemu pewien obszar w przestrzeni. Jak więc porównać położenia tych obiektów, a tym bardziej wyciągnąć wnioski o ich wzajemnym zasłanianiu. W skrajnym przypadku można wyobrazić sobie sytuację, że dwa obiekty zasłaniają się w taki sposób, że każdy jest częściowo zasłonięty przez drugi z nich. Do tego relacja częściowego zasłaniania nie jest relacją przechodnią. A zatem wyciągnięcie właściwego wniosku dotyczącego zasłaniania na podstawie wzajemnego położenia obiektów jest zadaniem trudnym. Znanych jest bardzo wiele różnych algorytmów rozstrzygania widoczności. W latach siedemdziesiątych i osiemdziesiątych XX wieku powstało ich rzeczywiście dużo. Warto wspomnieć przynajmniej o kilku z nich.

---

---

---

---

---

---

---

---

---

---

---

Zorientowanie ściany I Rozpatrzmy przypadek wielościanu wypukłego. Jest to jeden z przykładów problemu eliminacji elementów zasłoniętych, dla którego można pokazać kilka efektywnych i jednocześnie prostych algorytmów. Można zauważyć, że jeżeli na scenie jest dowolny wielościan wypukły (ale tylko jeden !), to wnioskowanie o widoczności jego elementów jest dość proste. Traktując taką scenę jako zbiór wielokątów (z których każdy jest oczywiście ścianą wielościanu), można ten zbiór podzielić na trzy grupy: 1. Wielokąty widoczne przez obserwatora (wielokąty przednie). 2. Wielokąty niewidoczne – zasłonięte (wielokąty tylne). 3. Wielokąty, których rzut jest odcinkiem. Wielokąty ostatniej grupy są pomijalne, odpowiednie odcinki zostaną i tak narysowane jeśli pojawią się wielokąty widoczne. W pierwszej i drugiej grupie występują wielokąty, które w całości podlegają określonym zasadom widoczności i przynależności do grupy. Nie może zachodzić przypadek, że tylko część wielokąta jest widoczna (a druga część zasłonięta). A zatem rozwiązanie zadania wybór elementów widocznych w przypadku wielościanu wypukłego sprowadza się do określenia zbioru wielokątów należących do pierwszej grupy. I one powinny być (w całości) narysowane. Można pokazać trzy (co najmniej) różne sposoby rozwiązanie tak zdefiniowanego zdania. Pierwszy sposób (Rozwiązanie A) polega na analizie położenia obiektów w przestrzeni. Definiowane są określone wektory a następnie jest wyznaczany iloczyn skalarny tych wektorów. Znak tego iloczynu określa przynależność do określonej grupy. Zwróćmy uwagę na fakt, że w tym przypadku nie ma w ogóle mowy o jakimkolwiek rzucie. Położenie obserwatora w przestrzeni w zupełności wystarczy.

---

---

---

---

---

---

---

---

---

---

---

Zorientowanie ściany II Rozwiązanie B korzysta z informacji zarówno pochodzących z przestrzeni obiektu (sceny), jak i z informacji jakie dostarcza rzut. – Porównywane jest zorientowanie ściany obiektu (w przestrzeni obiektu) i zorientowanie rzutu ściany (w przestrzeni rzutu). Jeśli oba zorientowania są jednakowe, to ściana jest widoczna (przednia).

---

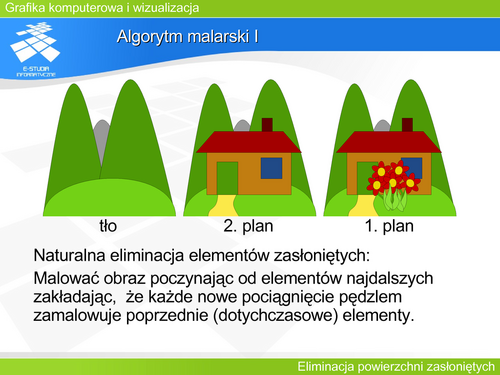
Bryła wypukła I Zadanie określenia widoczności elementów wielościanu wypukłego można więc rozwiązać na dwa sposoby korzystając z rozwiązań A i B sprawdzających zorientowanie poszczególnych ścian.

---

Bryła wypukła II Analizę widoczności w przypadku wielościanu wypukłego, można przeprowadzić opierając się tylko na informacji z przestrzeni rzutu – sposób C. W tym celu należy podzielić wierzchołki rzutu na dwa typy. Pierwszy typ charakteryzuje się tym, że węzeł oraz zewnętrzne krawędzie są widoczne. O pozostałych krawędziach i ich widoczności nie można nic powiedzieć. Drugi typ charakteryzuje się tym , że co prawda nie można stwierdzić czy węzeł jest widoczny czy nie, ale za to wszystkie elementy mają taki sam atrybut. A więc jeśli jakaś jedna krawędź jest widoczna, to cały węzeł i wszystkie jego krawędzie są widoczne.

---

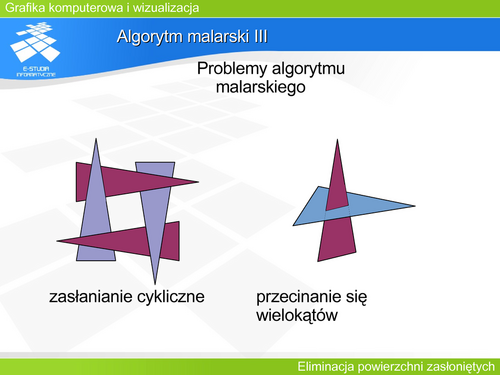
Bryła wypukła III Korzystając z klasyfikacji węzłów można zaproponować sposób C wyznaczania widoczności elementów wielościanu wypukłego. Określając widoczność jednego węzła drugiego typu można przenieść ten sam atrybut widoczności do sąsiednich węzłów, przechodząc od jednego węzła do drugiego. W ten sposób powstają dwa komplementarne obrazy. W takim postępowaniu nie jest potrzebna informacja z przestrzeni obiektu. Wystarczy tylko informacja dotycząca rzutu.

---

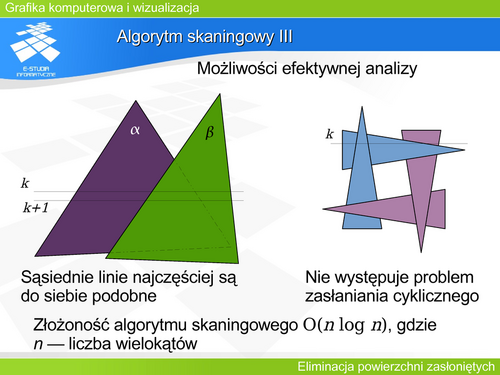
Klasy algorytmów Trzy sposoby rozwiązania problemu widoczności pokazują trzy sposoby wykorzystania informacji, pochodzących albo z przestrzeni obiektu (sceny), albo przestrzeni rzutu, albo obu. Oczywiście o ile w przypadku wielościanu wypukłego ten podział jest bardzo ostry i jednoznaczny, o tyle w przypadku dowolnego innego algorytmu podział będzie zdecydowanie mniej ostry i będzie oznaczał, że dany algorytm w większym stopniu wykorzystuje informację z jednej lub drugiej przestrzeni. Z drugiej strony często mówi się o precyzji obrazowej lub obiektowej danego algorytmu. Oznacza to, że algorytmy pracujące z precyzją obrazowa wykonują obliczenia z dokładnością urządzenia wyświetlającego (wynikającą z wyświetlania pojedynczego piksela). Algorytmy pracujące z precyzją obiektowa wykonują obliczenia z dokładnością związaną z definicją obiektów, a nie pikseli.

---

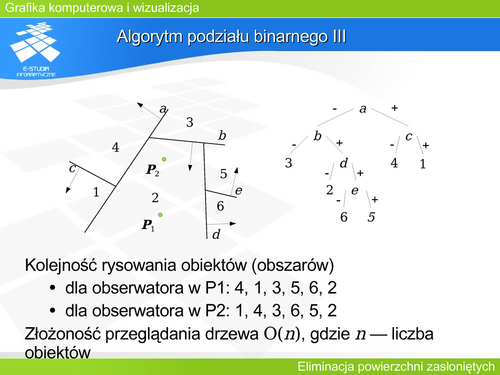
Bryła wypukła, złożoność algorytmów Aby określić złożoność algorytmów określania widoczności należy zdefiniować miarę złożoności sceny (obiektu). Najczęściej przyjmuje się, liczbę ścian jako taką miarę. Złożoność trzech wariantów algorytmów eliminacji elementów zasłoniętych dla wielościanu wypukłego jest liniowa. Jest to szczególny przypadek wśród algorytmów określania widoczności.

---

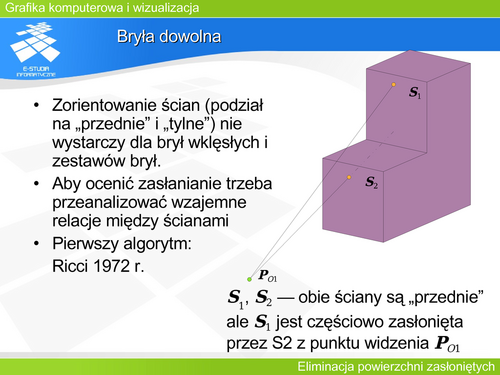
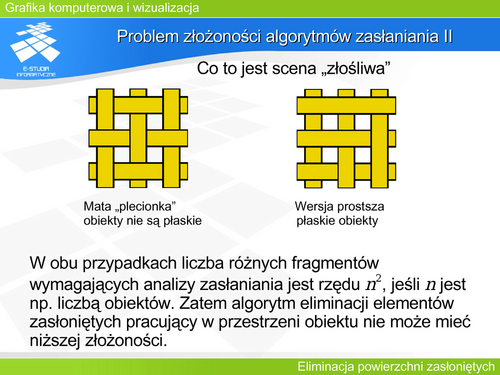
Bryła dowolna W przypadku bryły dowolnej lub zestawu dowolnych brył, podział ścian na przednie i tylne nie wystarczy, gdyż taka analiza nie uwzględnia wzajemnego zasłaniania ścian, jakie może wystąpić między obiektami lub ścianami tego samego obiektu. Problem taki występuje także dla zestawu brył wypukłych, tylko dla jednej bryły wypukłej można pokazać prostszy algorytm. Naturalnym podejściem jest analiza wzajemnego położenia ścian, ale w takim przypadku trzeba przeanalizować wszystkie pary ścian (analiza „każdy z każdym”). Prowadzi to oczywiście do kwadratowej złożoności obliczeniowej algorytmu. Najprostszym mechanizmem przyspieszającym takie postępowanie jest test MINMAX czyli „opakowanie” wielokątów prostopadłościanami definiującymi minimum i maksimum po każdej współrzędnej dla danego wielokąta. Porównując wzajemne położenie prostopadłościanów opakowujących (co jest prostsze gdyż jest porównaniem minimów i maksimów współrzędnych) można wyeliminować wiele przypadków, gdy wielościany nie mogą się zasłaniać. Oczywiście takie postępowanie nie zmienia asymptotycznej złożoności obliczeniowej. Test MINMAX jest często stosowany do różnych algorytmów eliminacji elementów zasłoniętych. Pierwszy algorytm rozstrzygania widoczności dla dowolnych brył, przy założeniu że ściany są trójkątami (a przecież dowolny wielokąt zawsze może zostać rozłożony na zbiór trójkątów) podał Ricci w 1972 roku. Był to algorytm pracujący metodą „każdy z każdym” o kwadratowej złożoności obliczeniowej.

---