MO Moduł 7: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 5: | Linia 5: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd2.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd2.png|thumb|500px]] | ||
|valign="top"|Jak się o tym zaraz przekonamy rozważania teoretyczne (i wzory) potrzebne do zrozumienia zasad działania metod kierunków poprawy nie są łatwe. Dla metod obszaru zaufania są nieco bardziej skomplikowane i dlatego omawiać ich nie będziemy | |valign="top"|Jak się o tym zaraz przekonamy rozważania teoretyczne (i wzory) potrzebne do zrozumienia zasad działania metod kierunków poprawy nie są łatwe. Dla metod obszaru zaufania są nieco bardziej skomplikowane i dlatego omawiać ich nie będziemy | ||
| Linia 17: | Linia 17: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd4.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd4.png|thumb|500px]] | ||
|valign="top"|Jak pamiętamy, przyjęliśmy, że gradient <math>\nabla f</math> jest wektorem wierszowym. Jego transpozycję do wektora kolumnowego oznacza się <math>\nabla^ | |valign="top"|Jak pamiętamy, przyjęliśmy, że gradient <math>\nabla f</math> jest wektorem wierszowym. Jego transpozycję do wektora kolumnowego oznacza się <math>\nabla^{\mathrm T}f</math> . | ||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd5.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd5.png|thumb|500px]] | ||
|valign="top"|A. Cauchy zaproponował w 1847 r. algorytm wykorzystujący w podobny sposób gradient do rozwiązywania układu równań nieliniowych | |valign="top"|A. Cauchy zaproponował '''w 1847 r.''' algorytm wykorzystujący w podobny sposób gradient do rozwiązywania układu równań nieliniowych | ||
|} | |} | ||
---- | ---- | ||
| Linia 78: | Linia 78: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd14.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd14.png|thumb|500px]] | ||
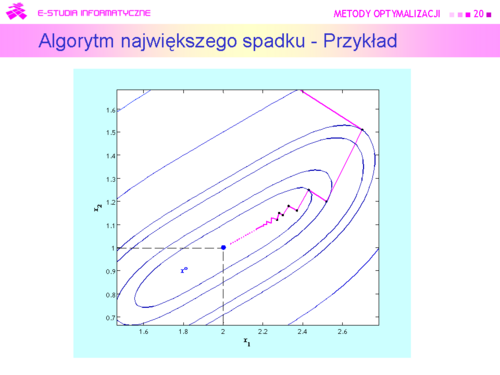
|valign="top"|Algorytm wykonał osiem kroków i zatrzymał się w punkcie <math>x^{(8)} = (2.27,1.12)</math> w którym <math>||\nabla f (2.27, 1.12)|| = 0.09</math>. Wartość funkcji celu <math>f (2.27,1.12) = 0.0062</math>, a odległość | |valign="top"|Algorytm wykonał osiem kroków i zatrzymał się w punkcie <math>x^{(8)} = (2.27,\,1.12)</math> w którym <math>||\nabla f (2.27,\, 1.12)|| = 0.09</math>. Wartość funkcji celu <math>f (2.27,\,1.12) = 0.0062</math>, a odległość<center><math>||x^{(8)} - x^o|| = 0.3</math>.</center> | ||
<math>||x^{(8)} | |||
|} | |} | ||
---- | ---- | ||
| Linia 97: | Linia 96: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd17.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd17.png|thumb|500px]] | ||
|valign="top"|Nie jest to przypadek. Zatrzymanie algorytmu relatywnie daleko od punktu minimalizującego wynika z właściwości funkcji, która w sporym otoczeniu minimum zmienia się niewiele (wartość poziomicy w punkcie <math>x^{(3)}</math> wynosi 0.09!). W konsekwencji zależności przyjęte w określeniu kryterium stopu szybko stają się niewielkie, co prowadzi do zbyt wczesnego (z punktu widzenia dokładności znalezienia punktu minimalizującego) zatrzymania algorytmu. | |valign="top"|Nie jest to przypadek. Zatrzymanie algorytmu relatywnie daleko od punktu minimalizującego wynika z właściwości funkcji, która w sporym otoczeniu minimum zmienia się niewiele (wartość poziomicy w punkcie <math>x^{(3)}</math> wynosi 0.09!). W konsekwencji zależności przyjęte w określeniu kryterium stopu szybko stają się niewielkie, co prowadzi do zbyt wczesnego (z punktu widzenia dokładności znalezienia punktu minimalizującego) zatrzymania algorytmu. | ||
| Linia 115: | Linia 114: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd20.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd20.png|thumb|500px]] | ||
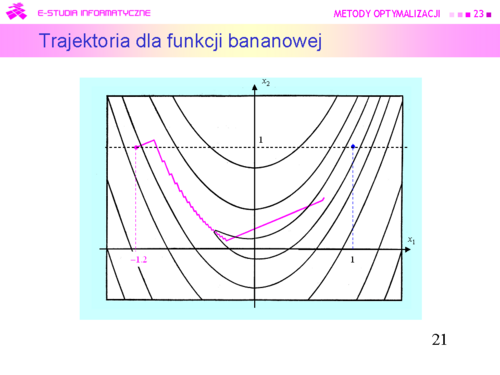
|valign="top"|Po „dużym skoku” z punktu początkowego, generowane kierunki są coraz bardziej prostopadłe do drogi która prowadzi do minimum, kroki są coraz krótsze i ruch algorytmu ma charakter zygzaka o coraz mniejszych wahaniach. | |valign="top"|Po „dużym skoku” z punktu początkowego, generowane kierunki są coraz bardziej prostopadłe do drogi która prowadzi do minimum, kroki są coraz krótsze i '''ruch algorytmu ma charakter zygzaka''' o coraz mniejszych wahaniach. | ||
|} | |} | ||
---- | ---- | ||
| Linia 133: | Linia 132: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd23.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd23.png|thumb|500px]] | ||
|valign="top"|Jak widać nie najlepiej. Algorytm szybko zaczął „zygzakować”, potem odważnie „wyskoczył” z doliny prowadzącej do minimum, lecz po powrocie na jej dno zaczął zmierzać do celu tak drobnymi zygzakami, że przez pozostałe 960 iteracji posunął się bardzo niewiele. „Odwaga” była tu przypadkowa. Od mniej więcej szóstej iteracji funkcja minimalizowana w kierunku <math>f_P</math> ma dwa minima lokalne, z których „dalsze” jest globalne. Do czterdziestej iteracji zastosowana metoda interpolacji kwadratowej znajdowała pierwsze minimum, w czterdziestej pierwszej – „przeskoczyła” to minimum i znalazła odległe minimum globalne. W tym przykładzie widać, że dokładna minimalizacja w kierunku może istotnie zmniejszyć ilość iteracji algorytmu największego spadku, ale nie wyeliminuje „zygzakowania | |valign="top"|Jak widać nie najlepiej. Algorytm szybko zaczął „zygzakować”, potem odważnie „wyskoczył” z doliny prowadzącej do minimum, lecz po powrocie na jej dno zaczął zmierzać do celu tak drobnymi zygzakami, że przez pozostałe 960 iteracji posunął się bardzo niewiele. „Odwaga” była tu przypadkowa. Od mniej więcej szóstej iteracji funkcja minimalizowana w kierunku <math>f_P</math> ma dwa minima lokalne, z których „dalsze” jest globalne. Do czterdziestej iteracji zastosowana metoda interpolacji kwadratowej znajdowała pierwsze minimum, w czterdziestej pierwszej – „przeskoczyła” to minimum i znalazła odległe minimum globalne. W tym przykładzie widać, że dokładna minimalizacja w kierunku może istotnie zmniejszyć ilość iteracji algorytmu największego spadku, ale nie wyeliminuje „zygzakowania". | ||
|} | |} | ||
---- | ---- | ||
| Linia 241: | Linia 240: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd41.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd41.png|thumb|500px]] | ||
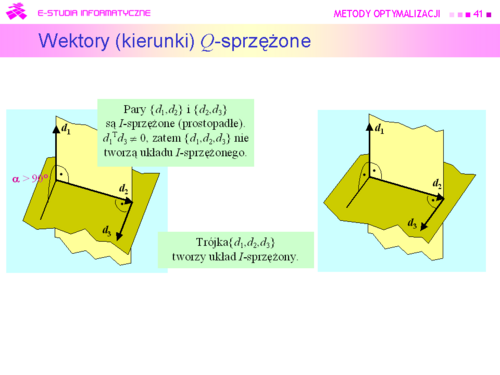
|valign="top"|Najprostszym przykładem dwu wektorów sprzężonych są wektory prostopadłe, które są sprzężone względem macierzy jednostkowej. Trzy wektory w przestrzeni trójwymiarowej są sprzężone względem macierzy jednostkowej jeżeli każdy z nich jest prostopadły do płaszczyzny wyznaczonej przez dwa pozostałe. Zatem już w przestrzeni trójwymiarowej sprzężenie względem macierzy jednostkowej to inna własność niż prostopadłość. | |valign="top"|Najprostszym przykładem dwu wektorów sprzężonych są wektory prostopadłe, które są sprzężone względem macierzy jednostkowej. Trzy wektory w przestrzeni trójwymiarowej są sprzężone względem macierzy jednostkowej jeżeli każdy z nich jest prostopadły do płaszczyzny wyznaczonej przez dwa pozostałe. Zatem już w przestrzeni trójwymiarowej sprzężenie względem macierzy jednostkowej to inna własność niż prostopadłość. | ||
| Linia 273: | Linia 272: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd46.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd46.png|thumb|500px]] | ||
|valign="top"|Wzory (43.A) i (46.A) pozwalają więc wyznaczyć dla zadania optymalizacji o kwadratowej funkcji celu z macierzą Q, posługując się tylko gradientami, kierunek sprzężony względem Q z początkowym kierunkiem antygradientu. | |valign="top"|Wzory (43.A) i (46.A) pozwalają więc wyznaczyć dla zadania optymalizacji o kwadratowej funkcji celu z macierzą <math>Q</math>, posługując się tylko gradientami, kierunek sprzężony względem <math>Q</math> z początkowym kierunkiem antygradientu. | ||
|} | |} | ||
---- | ---- | ||
| Linia 387: | Linia 386: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd65.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd65.png|thumb|500px]] | ||
|valign="top"|Dla zadań o kilku zmiennych zręczniej jest dokonywać odnowy co 3n lub co 2n kroków, ponieważ z odnową co n kroków działanie algorytmu dla takich zadań może różnić się niewiele od działania algorytmu największego spadku. | |valign="top"|Dla zadań o kilku zmiennych zręczniej jest dokonywać odnowy co <math>3n</math> lub co <math>2n</math> kroków, ponieważ z odnową co <math>n</math> kroków działanie algorytmu dla takich zadań może różnić się niewiele od działania algorytmu największego spadku. | ||
|} | |} | ||
---- | ---- | ||
| Linia 417: | Linia 416: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd70.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd70.png|thumb|500px]] | ||
|valign="top"|Przy odpowiednio mocniejszych założeniach o funkcji wyboru oraz wymaganiu dokładnej minimalizacji w kierunku, można pokazać, że algorytm ten zbiega superliniowo do punktu minimalizującego | |valign="top"|Przy odpowiednio mocniejszych założeniach o funkcji wyboru oraz wymaganiu dokładnej minimalizacji w kierunku, można pokazać, że algorytm ten zbiega <u> superliniowo</u> do punktu minimalizującego. | ||
|} | |} | ||
---- | ---- | ||
| Linia 429: | Linia 428: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd72.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd72.png|thumb|500px]] | ||
|valign="top"|Na rysunku zaznaczono kolorem zielonym „drogę” algorytmu gradientu sprzężonego z metodą interpolacji kwadratowej użytą do minimalizacji w kierunku, który wystartował z tego samego co poprzednio punktu początkowego <math>x^(0)=(0,3)</math> i miał znaleźć rozwiązanie z dokładnością <math>\ | |valign="top"|Na rysunku zaznaczono kolorem zielonym „drogę” algorytmu gradientu sprzężonego z metodą interpolacji kwadratowej użytą do minimalizacji w kierunku, który wystartował z tego samego co poprzednio punktu początkowego <math>x^{(0)}=(0,3)</math> i miał znaleźć rozwiązanie z dokładnością <math>\varepsilon = 0.05</math> (przypominamy, że dla algorytmu gradientu prostego wybrana dokładność była 2 razy mniejsza i wynosiła 0.1). Dla porównania kroki algorytmu największego spadku zaznaczono na czerwono.<br>Algorytm wykonał siedem kroków i zatrzymał się w punkcie <math>x^{(7)} = (2.185,\,1.094)</math> w którym <math>||\nabla f(2.185,\,1.094)||=0.02</math> . Wartość funkcji celu <math>f (2.185,\,1.094) = 0.0012</math>, a odległość proponowanego rozwiązania od punktu optymalnego jest równa<center><math>||x^{(7)}-x^o||= 0.208</math>.</center> | ||
Algorytm wykonał siedem kroków i zatrzymał się w punkcie <math>x^{(7)} = (2.185,1.094)</math> w którym <math>||\nabla f(2.185,1.094)||=0.02</math> . Wartość funkcji celu <math>f (2.185,1.094) = 0.0012</math>, a odległość proponowanego rozwiązania od punktu optymalnego jest równa | Krok pierwszy z <math>x^{(0)}=(0,\,3)</math> do <math>x^{(1)}=(2.70,\,1.51)</math> był oczywiście taki sam jak dla metody gradientu prostego. Przejście z kroku szóstego do siódmego jest na rysunku niezauważalne, ponieważ <math>x^{(6)} = (2.190,\,1.090)</math>. Zadanie jest dwuwymiarowe, zatem odnowa (ruch w kierunku antygradientu) nastąpiła w kroku trzecim, piątym i ostatnim – siódmym. Ponieważ punkty <math> x^{(2)}</math> wyznaczone w drugim kroku przez oba algorytmy leżą jeszcze blisko siebie to i antygradienty są prawie równe, więc ruch obu algorytmów w trzecim kroku musi dać punkty <math>x^{(3)}</math>, które też będą leżały blisko siebie. Lecz antygradient policzony w punkcie <math>x^{(3)}</math> wyliczonym przez algorytm najszybszego spadku jest równy <math>[-0.18\,\vdots -0.28]</math>, a kierunek poprawy wyznaczony w swoim punkcie <math>x^{(3)}</math> przez algorytm gradientu sprzężonego jest równy <math>[-0.30\,\vdots -0.25]</math>. Ta różnica spowodowała, że algorytm gradientu sprzężonego wyznaczył jako punkt <math>x^{(4)}</math> punkt o współrzędnych <math>(2.25,\,1.10)</math>, co dało wartość funkcji celu <math>f (2.25,\,1.10) = 0.0064</math>, a algorytm gradientu prostego – punkt o współrzędnych <math>(2.37,\,1.16)</math> z wartością funkcji celu <math>f(2.37,\,1.16) = 0.02</math>. W piątym kroku algorytm gradientu sprzężonego wyznaczył punkt <math>x^{(5)} = (2.23,\,1.12)</math> dający wartość funkcji celu <math>f(2.23,\,1.12) = 0.003</math> i wartość normy gradientu <math>||\nabla f(2.23,\,1.12)||=0.05</math> , a więc punkt lepszy niż ostatni (ósmy) punkt uzyskany przez algorytm najszybszego spadku (przypominamy był to punkt <math>(2.27,\,1.12)</math> w którym <math>f (2.27,\,1.12) = 0.0062</math>, oraz <math>||\nabla f(2.27,\,1.12)||=0.09</math> . | ||
<math>||x^{(7)}-x^ | |||
Krok pierwszy z <math>x^{(0} | |||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd73.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd73.png|thumb|500px]] | ||
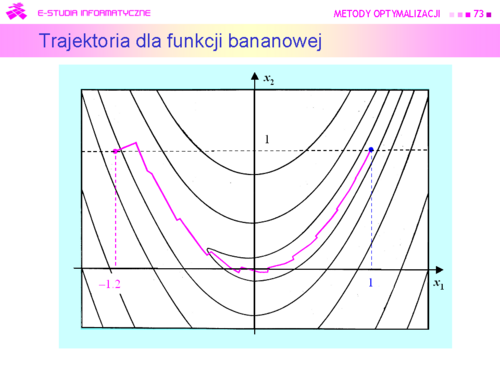
|valign="top"|Rysunek pokazuje kolejne kroki algorytmu gradientu sprzężonego szukającego minimum funkcji Rosenbrocka. Algorytm jest bez odnowy (bo funkcja Rosenbrocka jest dwuwymiarowa) i z minimalizacją w kierunku wykorzystującą wielomian interpolacyjny. Algorytm wykonał 24 iteracje poruszając się po dnie doliny bez zygzakowania i dość szybko w kierunku punktu minimalizującego | |valign="top"|Rysunek pokazuje kolejne kroki algorytmu gradientu sprzężonego szukającego minimum funkcji Rosenbrocka. Algorytm jest bez odnowy (bo funkcja Rosenbrocka jest dwuwymiarowa) i z minimalizacją w kierunku wykorzystującą wielomian interpolacyjny. Algorytm wykonał 24 iteracje poruszając się po dnie doliny bez zygzakowania i dość szybko w kierunku punktu minimalizującego | ||
| Linia 526: | Linia 520: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd87.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd87.png|thumb|500px]] | ||
|valign="top"|Oznacza to, że zastosowanie metody stycznych Newtona do rozwiązywania zadania optymalizacji to nic innego jak przyjęcie, że bieżące przybliżenie kwadratowe (84.A) dobrze opisuje zachowanie funkcji minimalizowanej w otoczeniu każdego punktu bieżącego. Zatem z bieżącego punktu należy przejść do punktu w którym funkcja aproksymująca osiąga minimum. W pobliżu lokalnego minimum funkcji celu na pewno takie postępowanie doprowadzi do tego minimum, ale w dużej odległości od niego tak być nie musi, stąd wspomniana wada metody Newtona – gwarantowana zbieżność tylko wtedy gdy algorytm wystartuje w stosownym otoczeniu rozwiązania | |valign="top"|Oznacza to, że zastosowanie metody stycznych Newtona do rozwiązywania zadania optymalizacji to nic innego jak przyjęcie, że bieżące przybliżenie kwadratowe (84.A) dobrze opisuje zachowanie funkcji minimalizowanej w otoczeniu każdego punktu bieżącego. Zatem z bieżącego punktu należy przejść do punktu w którym funkcja aproksymująca osiąga minimum. W pobliżu lokalnego minimum funkcji celu na pewno takie postępowanie doprowadzi do tego minimum, ale w dużej odległości od niego tak być nie musi, stąd wspomniana wada metody Newtona – gwarantowana zbieżność tylko wtedy gdy algorytm wystartuje w stosownym otoczeniu rozwiązania | ||
| Linia 562: | Linia 556: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd93.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd93.png|thumb|500px]] | ||
|valign="top"|Analiza równania (92.A) i wymagania (93,A) pokazała, że poprawka <math>V^{(k)}</math> nie jest określona przez nie jednoznacznie, stąd opracowano wiele wzorów na poprawkę. Z teoretycznego punktu widzenia najciekawsza jest tzw. rodzina poprawek Broydena. | |valign="top"|Analiza równania (92.A) i wymagania (93,A) pokazała, że poprawka <math>V^{(k)}</math> nie jest określona przez nie jednoznacznie, stąd opracowano wiele wzorów na poprawkę. Z teoretycznego punktu widzenia najciekawsza jest tzw. '''rodzina poprawek Broydena'''. | ||
|} | |} | ||
---- | ---- | ||
| Linia 586: | Linia 580: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd97.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd97.png|thumb|500px]] | ||
|valign="top"|W 1972 r. L.C.W. Dixon pokazał, że z teoretycznego punktu widzenia wszystkie poprawki rodziny Broydena są równoważne – przy dokładnej minimalizacji w kierunku kolejne punkty <math>x^{(k)}</math> obliczone według wzorów (96.A) są przy użyciu dowolnej z nich takie same. | |valign="top"|W 1972 r. L.C.W. Dixon pokazał, że z teoretycznego punktu widzenia wszystkie poprawki rodziny Broydena są równoważne – przy dokładnej minimalizacji w kierunku kolejne punkty <math>x^{(k)}</math> obliczone według wzorów (96.A) są przy użyciu dowolnej z nich takie same. | ||
| Linia 604: | Linia 598: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd100.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd100.png|thumb|500px]] | ||
|valign="top"|Twierdzenie (7.2QN) wskazuje na związek miedzy algorytmami quasi-newtonowskimi i algorytmami gradientu sprzężonego. Można też wskazać i różnice. | |valign="top"|Twierdzenie (7.2QN) wskazuje na związek miedzy algorytmami quasi-newtonowskimi i algorytmami gradientu sprzężonego. Można też wskazać i różnice. | ||
| Linia 700: | Linia 694: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M7_Slajd116.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M7_Slajd116.png|thumb|500px]] | ||
|valign="top"|Algorytm gradientu sprzężonego zużył 24 iteracje na dotarcie do rozwiązania, a quasi-newtonowskiemu algorytmowi BFGS wystarczyło tylko 11 iteracji. | |valign="top"|Algorytm gradientu sprzężonego zużył 24 iteracje na dotarcie do rozwiązania, a quasi-newtonowskiemu algorytmowi BFGS wystarczyło tylko 11 iteracji. | ||
Wersja z 12:56, 10 paź 2006
 |
 |
 |
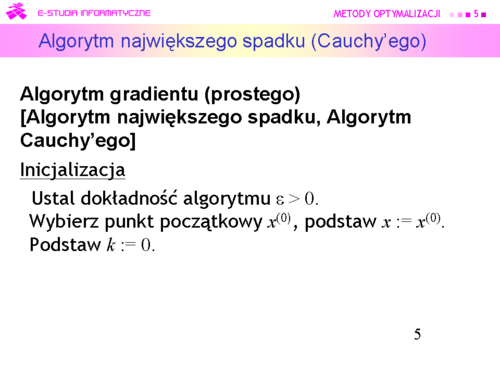
Jak pamiętamy, przyjęliśmy, że gradient jest wektorem wierszowym. Jego transpozycję do wektora kolumnowego oznacza się . |
 |
A. Cauchy zaproponował w 1847 r. algorytm wykorzystujący w podobny sposób gradient do rozwiązywania układu równań nieliniowych |
 |
 |
 |
 |
 |
 |
 |
 |
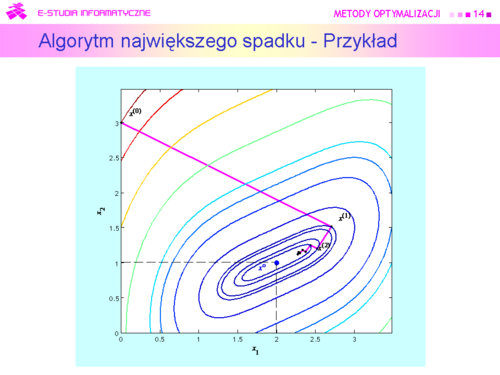 |
Algorytm wykonał osiem kroków i zatrzymał się w punkcie w którym . Wartość funkcji celu , a odległość |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
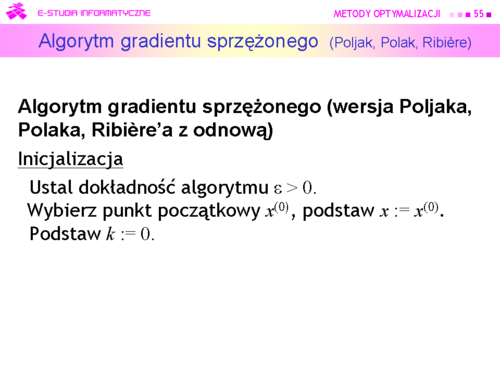 |
 |
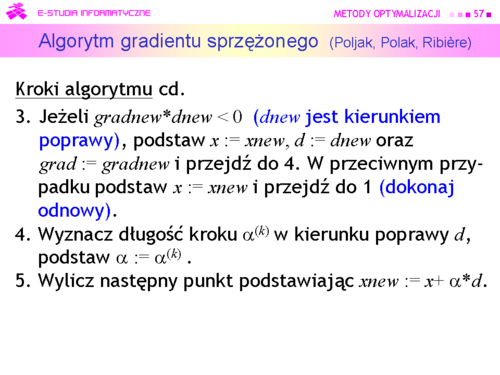 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Przy odpowiednio mocniejszych założeniach o funkcji wyboru oraz wymaganiu dokładnej minimalizacji w kierunku, można pokazać, że algorytm ten zbiega superliniowo do punktu minimalizującego. |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
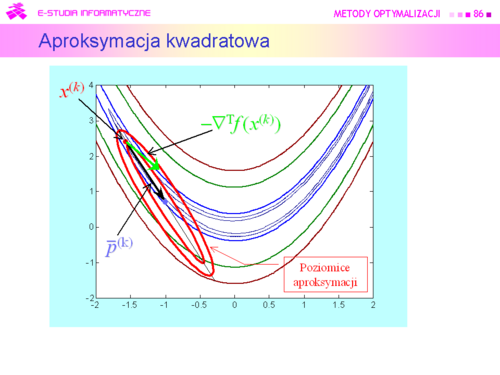 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Twierdzenie (7.2QN) wskazuje na związek miedzy algorytmami quasi-newtonowskimi i algorytmami gradientu sprzężonego. Można też wskazać i różnice. |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
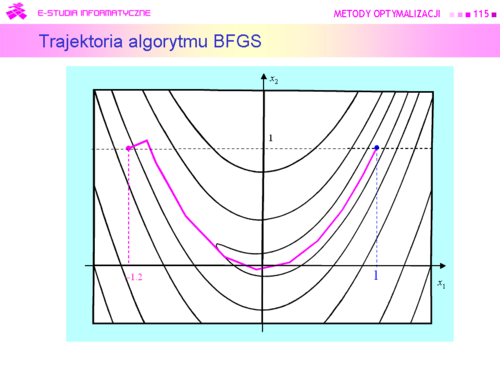 |
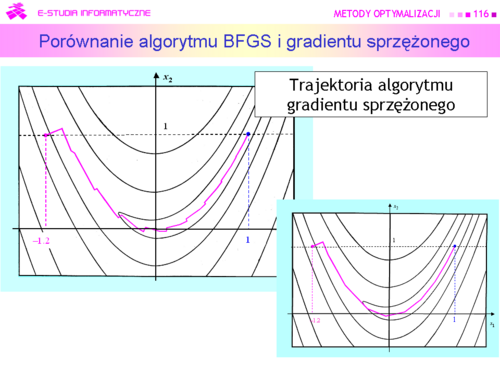 |
Algorytm gradientu sprzężonego zużył 24 iteracje na dotarcie do rozwiązania, a quasi-newtonowskiemu algorytmowi BFGS wystarczyło tylko 11 iteracji. |
 |
 |