MO Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 143: | Linia 143: | ||
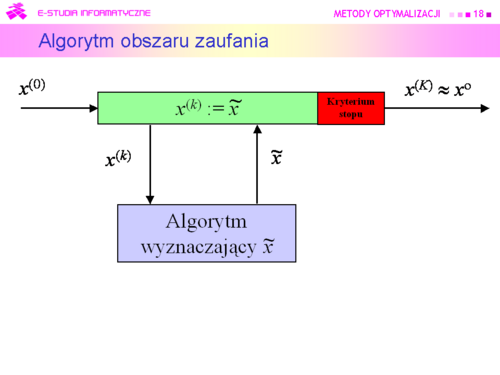
Kroki algorytmu | Kroki algorytmu | ||
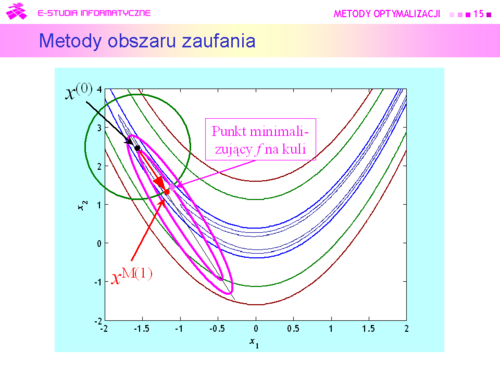
#Dla punktu <math>x^{(k)}</math> wyznacz model <math>f_M(\cdot; x^{(k)})</math> funkcji celu w jego otoczeniu. | #Dla punktu <math>x^{(k)}</math> wyznacz model <math>f_M(\cdot; x^{(k)})</math> funkcji celu w jego otoczeniu. | ||
#Znajdź przybliżenie <math>\tilde{x}^{(k)}</math> punktu | #Znajdź przybliżenie <math>\tilde{x}^{(k)}</math> punktu <math>x^{M(k)}</math> = arg min<math>_{x\epsilon T(x^{(k)})}f_M(x;x^{(k)})</math>. | ||
<math>x^{M(k)}</math> = arg min<math>_{x\epsilon T(x^{(k)})}f_M(x;x^{(k)})</math>. | |||
#Sprawdź czy wielkość obszaru zaufania została wybrana właściwie. Jeżeli tak, podstaw <math>x^{(k)} :=\tilde x^{(k)}</math> , idź do 5. W przeciwnym przypadku idź do 4. | #Sprawdź czy wielkość obszaru zaufania została wybrana właściwie. Jeżeli tak, podstaw <math>x^{(k)} :=\tilde x^{(k)}</math> , idź do 5. W przeciwnym przypadku idź do 4. | ||
#Zmniejsz obszar zaufania do <math>TS</math>, podstaw <math>T(x^{(k)}) := TS</math>, idź do 2. | #Zmniejsz obszar zaufania do <math>TS</math>, podstaw <math>T(x^{(k)}) := TS</math>, idź do 2. | ||
| Linia 204: | Linia 203: | ||
{| border="0" cellpadding="4" width="125%" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd26.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd26.png|thumb|500px]] | ||
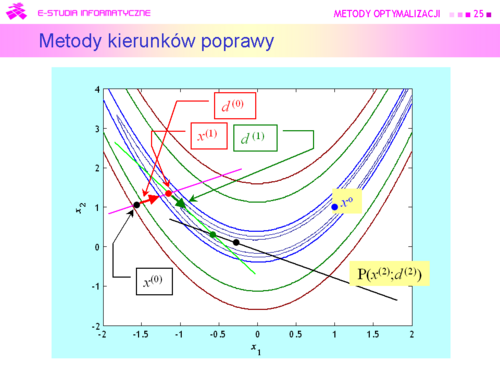
|valign="top"|Dokonujemy, jak mówimy '''minimalizacji w kierunku'''. Formułując to zadanie przybliżonej minimalizacji funkcji jednej zmiennej <math>\alpha (x^{(k)}</math> i <math>d</math> są ustalone!) wykorzystaliśmy fakt, że zbiór dopuszczalny <math>P(x(^{k)};d)</math> jest określony jednym ograniczeniem równościowym. | |valign="top"|Dokonujemy, jak mówimy '''minimalizacji w kierunku'''. Formułując to zadanie przybliżonej minimalizacji funkcji jednej zmiennej <math>\alpha</math> (<math>x^{(k)}</math> i <math>d</math> są ustalone!) wykorzystaliśmy fakt, że zbiór dopuszczalny <math>P(x(^{k)};d)</math> jest określony jednym ograniczeniem równościowym. | ||
Wprawdzie wiemy, że „ruszanie się” wzdłuż kierunku poprawy nie musi doprowadzić do minimum globalnego, ale na pewno poprawi wartość funkcji celu. O ile poprawi ? – Może poprawić bardzo niewiele, ale tak jak przy ustalaniu podstaw poprzednich metod, zgodnie z naszym podejściem optymistycznym, uważamy że ta poprawa będzie istotna. Jak pamiętamy przekonanie to ma podstawy formalne, ponieważ rozważania teoretyczne sugerują, że „porządne” funkcje są lokalnie wypukłe, a co za tym idzie nie powinno być kłopotów ze znalezieniem punktu lepszego niż bieżący. Przy wymyślaniu kryterium stopu pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o jakąś miarę „małości” gradientu. | Wprawdzie wiemy, że „ruszanie się” wzdłuż kierunku poprawy nie musi doprowadzić do minimum globalnego, ale na pewno poprawi wartość funkcji celu. O ile poprawi ? – Może poprawić bardzo niewiele, ale tak jak przy ustalaniu podstaw poprzednich metod, zgodnie z naszym podejściem optymistycznym, uważamy że ta poprawa będzie istotna. Jak pamiętamy przekonanie to ma podstawy formalne, ponieważ rozważania teoretyczne sugerują, że „porządne” funkcje są lokalnie wypukłe, a co za tym idzie nie powinno być kłopotów ze znalezieniem punktu lepszego niż bieżący. Przy wymyślaniu kryterium stopu pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o jakąś miarę „małości” gradientu. | ||
Wersja z 14:27, 5 paź 2006
 |
 |
 |
 |
 |
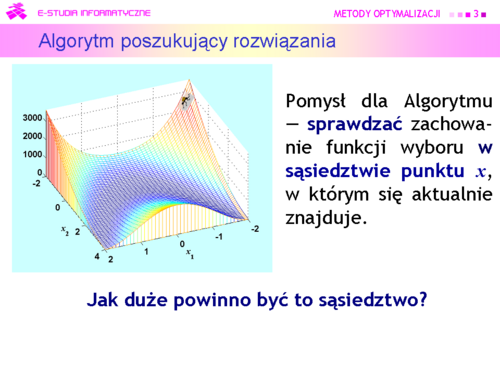
Algorytm może być:
a następnie przeszukiwać je tak jak poprzednio. |
 |
 |
Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez:
J. A. Neldera i R. Meada i opublikowany w 1965 r. |
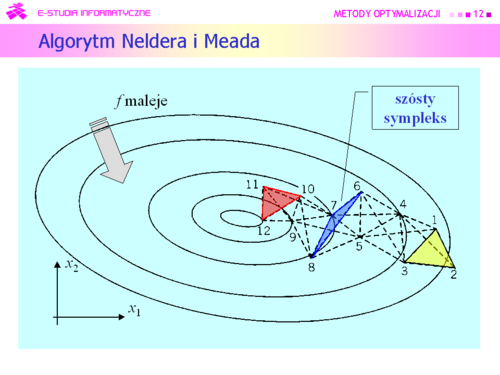 |
Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. |
 |
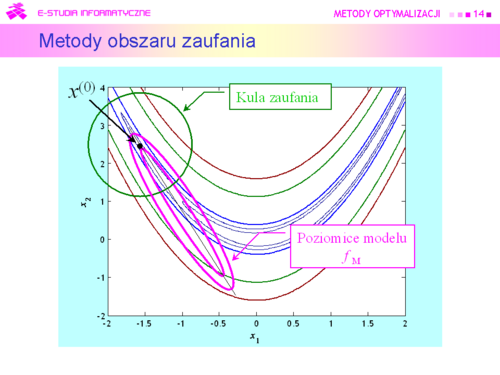
Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się:
Metodami obszaru zaufania (Trust region methods) |
 |
 |
 |
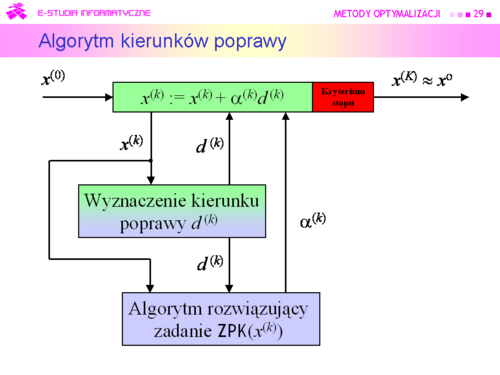
Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3).
Algorytm będzie zatem wykorzystywał: Metody kierunków poprawy |
 |
 |
 |
 |
Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający “optymalność” kolejnego punktu, a drugi określający maksymalną liczbę iteracji. |
 |
 |
 |
 |
 |
 |