MO Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 184: | Linia 184: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd23.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd23.png|thumb|500px]] | ||
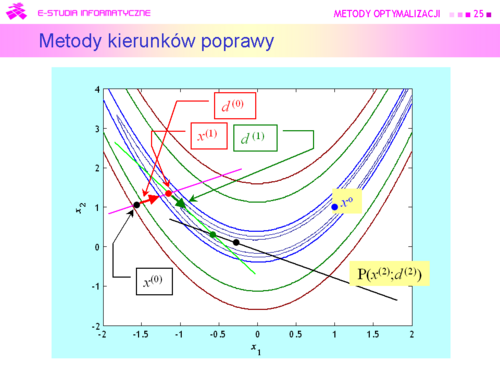
|valign="top"|Gdy znamy gradient, nierówność ta pozwala sprawdzić czy dany kierunek d jest kierunkiem poprawy. Mając ustalony kierunek poprawy powinniśmy poruszając się wzdłuż niego znaleźć punkt dający mniejszą niż w punkcie bieżącym wartość funkcji celu. | |valign="top"|Gdy znamy gradient, nierówność ta pozwala sprawdzić czy dany kierunek d jest kierunkiem poprawy. Mając ustalony kierunek poprawy powinniśmy poruszając się wzdłuż niego znaleźć punkt dający mniejszą niż w punkcie bieżącym wartość funkcji celu. | ||
| Linia 196: | Linia 196: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd25.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd25.png|thumb|500px]] | ||
|valign="top"|Zgodnie z określeniem poruszania się wzdłuż kierunku, znalezienie punktu <math>\bar{x} \in P(x^{(k)};d)\subset R^n</math> jest równoważne ustaleniu pewnego <math>\bar{\alpha} \in R</math> Zatem zmieniając <math>\alpha </math> od zera do plus nieskończoności ruszamy się wzdłuż prostej <math>P(x^{(k)};d)</math> w kierunku malenia funkcji celu. Konkretną wartość <math>\bar{\alpha}</math> – długość kroku – możemy ustalić a priori. Intuicyjnie nie jest to najlepszy sposób, bo żeby zabezpieczyć się przed zbytnim przeskoczeniem minimum funkcji celu na zbiorze P(x(k);d) trzeba tą stałą długość kroku wybrać niewielką. Wobec tego można postępować tak: wybieramy duży krok początkowy <math>\alpha ^{(0)}</math>, gdy <math>f(x^{(k)}+\alpha ^{(0)}d)<f(x^{(k)})</math> to <math>\alpha^{(0)}</math> uznajemy za długość kroku, gdy przeciwnie – zmniejszamy <math>\alpha^{(0)}</math> do <math>\alpha^{(1)}</math>), powtarzamy sprawdzenie czy wartość funkcji zmalała, itd. aż uzyskamy krok dający poprawę | |valign="top"|Zgodnie z określeniem poruszania się wzdłuż kierunku, znalezienie punktu <math>\bar{x} \in P(x^{(k)};d)\subset R^n</math> jest równoważne ustaleniu pewnego <math>\bar{\alpha} \in R</math> Zatem zmieniając <math>\alpha </math> od zera do plus nieskończoności ruszamy się wzdłuż prostej <math>P(x^{(k)};d)</math> w kierunku malenia funkcji celu. Konkretną wartość <math>\bar{\alpha}</math> – długość kroku – możemy ustalić a priori. Intuicyjnie nie jest to najlepszy sposób, bo żeby zabezpieczyć się przed zbytnim przeskoczeniem minimum funkcji celu na zbiorze P(x(k);d) trzeba tą stałą długość kroku wybrać niewielką. Wobec tego można postępować tak: wybieramy duży krok początkowy <math>\alpha ^{(0)}</math>, gdy <math>f(x^{(k)}+\alpha ^{(0)}d)<f(x^{(k)})</math> to <math>\alpha^{(0)}</math> uznajemy za długość kroku, gdy przeciwnie – zmniejszamy <math>\alpha^{(0)}</math> do <math>\alpha^{(1)}</math>), powtarzamy sprawdzenie czy wartość funkcji zmalała, itd. aż uzyskamy krok dający poprawę | ||
| Linia 202: | Linia 202: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd26.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd26.png|thumb|500px]] | ||
|valign="top"|Dokonujemy, jak mówimy minimalizacji w kierunku. Formułując to zadanie przybliżonej minimalizacji funkcji jednej zmiennej <math>\alpha (x^{(k)}</math> i d są ustalone!) wykorzystaliśmy fakt, że zbiór dopuszczalny <math>P(x(^{k)};d)</math> jest określony jednym ograniczeniem równościowym. | |valign="top"|Dokonujemy, jak mówimy '''minimalizacji w kierunku'''. Formułując to zadanie przybliżonej minimalizacji funkcji jednej zmiennej <math>\alpha (x^{(k)}</math> i <math>d</math> są ustalone!) wykorzystaliśmy fakt, że zbiór dopuszczalny <math>P(x(^{k)};d)</math> jest określony jednym ograniczeniem równościowym. | ||
Wprawdzie wiemy, że „ruszanie się” wzdłuż kierunku poprawy nie musi doprowadzić do minimum globalnego, ale na pewno poprawi wartość funkcji celu. O ile poprawi ? – Może poprawić bardzo niewiele, ale tak jak przy ustalaniu podstaw poprzednich metod, zgodnie z naszym podejściem optymistycznym, uważamy że ta poprawa będzie istotna. Jak pamiętamy przekonanie to ma podstawy formalne, ponieważ rozważania teoretyczne sugerują, że „porządne” funkcje są lokalnie wypukłe, a co za tym idzie nie powinno być kłopotów ze znalezieniem punktu lepszego niż bieżący. Przy wymyślaniu kryterium stopu pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o jakąś miarę „małości” gradientu. | Wprawdzie wiemy, że „ruszanie się” wzdłuż kierunku poprawy nie musi doprowadzić do minimum globalnego, ale na pewno poprawi wartość funkcji celu. O ile poprawi ? – Może poprawić bardzo niewiele, ale tak jak przy ustalaniu podstaw poprzednich metod, zgodnie z naszym podejściem optymistycznym, uważamy że ta poprawa będzie istotna. Jak pamiętamy przekonanie to ma podstawy formalne, ponieważ rozważania teoretyczne sugerują, że „porządne” funkcje są lokalnie wypukłe, a co za tym idzie nie powinno być kłopotów ze znalezieniem punktu lepszego niż bieżący. Przy wymyślaniu kryterium stopu pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o jakąś miarę „małości” gradientu. | ||
| Linia 222: | Linia 222: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd29.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd29.png|thumb|500px]] | ||
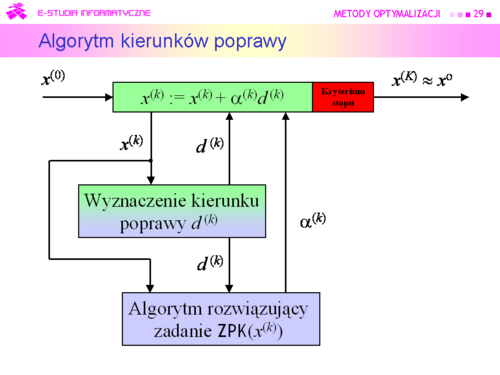
|valign="top"|Bardziej formalnie przedstawioną procedurę minimalizacji opartą na generowaniu kierunków poprawy opisuje następujący podstawowy algorytm kierunków poprawy. | |valign="top"|Bardziej formalnie przedstawioną procedurę minimalizacji opartą na generowaniu kierunków poprawy opisuje następujący podstawowy algorytm kierunków poprawy. | ||
Podstawowy algorytm kierunków poprawy | |||
'''Podstawowy algorytm kierunków poprawy''' | |||
Inicjalizacja | Inicjalizacja | ||
| Linia 242: | Linia 243: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd30.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd30.png|thumb|500px]] | ||
|valign="top"|Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający “optymalność” kolejnego punktu, a drugi określający maksymalną | |valign="top"|Teraz zauważmy tylko, że '''test stopu''' powinien zawierać dwa warunki: jeden '''badający “optymalność”''' kolejnego punktu, a drugi określający '''maksymalną liczbę iteracji'''. | ||
|} | |} | ||
---- | ---- | ||
| Linia 254: | Linia 255: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd32.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd32.png|thumb|500px]] | ||
|valign="top"|Szukanie punktu dającego poprawę: | |valign="top"|Szukanie punktu dającego poprawę: | ||
*w metodzie rozsiewania punktów próbnych jest to zadanie wyboru punktu najmniejszego ze skończonej ich liczby; | *w metodzie rozsiewania punktów próbnych jest to zadanie wyboru punktu najmniejszego ze skończonej ich liczby; | ||
*w metodzie obszarów zaufania jest to zadanie wielo-wymiarowej minimalizacji przy ograniczeniach, najczęściej funkcji kwadratowej, zadanie ZKK; | *w metodzie obszarów zaufania jest to zadanie wielo-wymiarowej minimalizacji przy ograniczeniach, najczęściej funkcji kwadratowej, zadanie '''ZKK'''; | ||
*dla metody kierunków poprawy jest to poszukiwanie punktu dającego akceptowalne zmalenie w stosunku do wartości w zerze (punkcie początkowym), odpowiednio określonej funkcji jednej zmiennej, zadanie ZPK. | *dla metody kierunków poprawy jest to poszukiwanie punktu dającego akceptowalne zmalenie w stosunku do wartości w zerze (punkcie początkowym), odpowiednio określonej funkcji jednej zmiennej, zadanie '''ZPK'''. | ||
|} | |} | ||
| Linia 270: | Linia 271: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd34.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd34.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Zbieżność skończona, która ma miejsce wtedy gdy istnieje taka liczba K dla której <math>x | *'''Zbieżność skończona''', która ma miejsce wtedy gdy istnieje taka liczba <math>K</math> dla której <math>x^{(K)} = x^o</math>. Z punktu widzenia znajdowania rozwiązań zadań optymalizacji wydaje się, że to najlepszy rodzaj zbieżności. Taki rodzaj zbieżności ma algorytm Simplex rozwiązywania zadań liniowych. Jednak jak pamiętamy, liczba iteracji może być bardzo duża, co oznacza, że na rozwiązanie zadania trzeba bardzo długo czekać. Metody punktu wewnętrznego nie mają skończonej zbieżności jednak dają zadowalające przybliżenie rozwiązania dużo szybciej. Dlatego wciąż trwają poszukiwania coraz bardziej skutecznych metod tego typu. A wniosek ogólny – z praktycznego punktu widzenia zbieżność skończona z bardzo dużym <math>K</math> może być gorsza niż zbieżność nieskończona, w sytuacji w której ciąg szybko zmierza do niewielkiego otoczenia rozwiązania. | ||
*Znana Państwu z analizy matematycznej zbieżność wektorowego ciągu nieskończonego, zwana jest w teorii metod optymalizacji krótko zbieżnością (nieskończoną). Jest ona rozumiana dwojako: jako zbieżność do rozwiązania <math>x^o</math>, albo dla funkcji gładkich – zbieżność do punktu stacjonarnego gradientu, tzn. takiego wektora <math>\hat{x}</math> , że | *Znana Państwu z analizy matematycznej '''zbieżność wektorowego ciągu nieskończonego''', zwana jest w teorii metod optymalizacji krótko '''zbieżnością''' (nieskończoną). Jest ona rozumiana dwojako: jako '''zbieżność do rozwiązania''' <math>x^o</math>, albo dla funkcji gładkich – '''zbieżność do punktu stacjonarnego gradientu''', tzn. takiego wektora <math>\hat{x}</math>, że <math>\nabla f (\hat{x})=0</math>. Jak pamiętamy punkt <math>\hat{x}</math> może być punktem lokalnego minimum, maksimum albo lokalne zachowanie funkcji w różnych kierunkach może być różne, np. może to być punkt siodłowy albo punkt przegięcia. Ten ostatni przypadek pokazuje rysunek na następnej stronie. | ||
*Dlatego w niektórych wypadkach twórcom algorytmów udaje się udowodnić własność jeszcze słabszą: '''ciąg''' wektorów generowany przez algorytm '''zawiera podciąg zbieżny'''. Akceptacja zbieżności tego rodzaju po pokazaniu na przykładach, że algorytm w rozsądnej liczbie kroków (iteracji) znajduje dobre przybliżenie rozwiązania mieści się w przyjętym “optymistycznym” podejściu do analizy sytuacji. | |||
<math>\nabla f (\hat{x})=0</math> | |||
Jak pamiętamy punkt | |||
*Dlatego w niektórych wypadkach twórcom algorytmów udaje się udowodnić własność jeszcze słabszą: ciąg wektorów generowany przez algorytm zawiera podciąg zbieżny. | |||
Akceptacja zbieżności | |||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd35.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd35.png|thumb|500px]] | ||
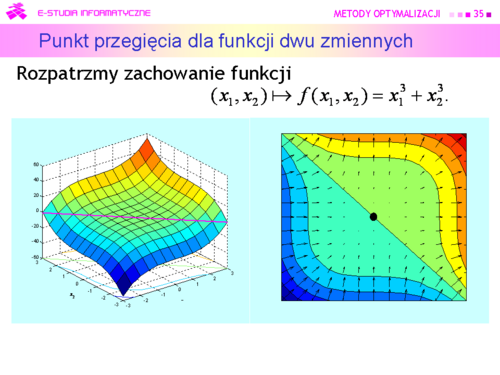
|valign="top"|W tym przypadku rozwiązaniem równania <math>\nabla f (\hat{x})=0</math> jest <math>\hat{x}=(0,0)</math> , a ten punkt ekstremum, nawet lokalnym, dla rozważanej funkcji nie jest. Jednak nasze optymistyczne podejście pozwala przyjąć, że przypadki takie jak przedstawiony, są bardzo rzadkie. | |valign="top"|W tym przypadku rozwiązaniem równania <math>\nabla f (\hat{x})=0</math> jest <math>\hat{x}=(0,0)</math> , a ten punkt ekstremum, nawet lokalnym, dla rozważanej funkcji nie jest. Jednak nasze optymistyczne podejście pozwala przyjąć, że przypadki takie jak przedstawiony, są bardzo rzadkie. | ||
| Linia 297: | Linia 293: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd37.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd37.png|thumb|500px]] | ||
|valign="top"|Zbieżny ciąg <math>{x^{(k)}^\infty_{k=0}}</math> otrzymany w kolejnych krokach algorytmu, jest zbieżny | |valign="top"|'''Zbieżny''' ciąg <math>\{x^{(k)}\}^\infty_{k=0}}</math> otrzymany w kolejnych krokach algorytmu, jest zbieżny | ||
a) liniowo, gdy dodatkowo | a) '''liniowo''', gdy dodatkowo | ||
<math>\frac{||x^{(k+1)-x^o | lim<math>_{k\rightarrow\infty}\frac{||x^{(k+1)}-x^o||}{||x^{(k)}-x^o||} = \rho > 0</math>, | ||
b) superliniowo, gdy dodatkowo | b) '''superliniowo''', gdy dodatkowo | ||
<math>\frac{||x^{(k+1)-x^o | lim<math>_{k\rightarrow\infty}\frac{||x^{(k+1)}-x^o||}{||x^{(k)}-x^o||} = 0</math>, | ||
c) kwadratowo, gdy dodatkowo | c) '''kwadratowo''', gdy dodatkowo | ||
<math>\frac{||x^{(k+1)-x^o | lim<math>_{k\rightarrow\infty}\frac{||x^{(k+1)}-x^o||}{||x^{(k)}-x^o||^2}\ = \rho \geq 0</math>. | ||
Definicje szybkości związane są z szybkością zbiegania do zera: | Definicje szybkości związane są z szybkością zbiegania do zera: | ||
<math>h^{(k)}=2^{-k} | ''postępu geometrycznego'' o dodatnim ilorazie mniejszym niż jeden, np. danego wzorem | ||
<math>h^{(k)} = 2^{-k}</math>, bo <math>\frac{2^{-(k+1)}}{2^{-k}}=\frac{1}{2} > 0</math> – ''zbieżność liniowa'', | |||
np. ciągu danego wzorem | np. ciągu danego wzorem | ||
<math>h^{(k)}=k^{-k},k\ | <math>h^{(k)}=k^{-k},k \geq 1</math>, bo <math>\frac{k^{-(k+1)}}{k^k}=\frac{1}{k}\rightarrow 0</math> – ''zbieżność superliniowa'', | ||
np. ciągu danego wzorem | np. ciągu danego wzorem | ||
<math>h^{(k)}=2^{-k},k\ | <math>h^{(k)}=2^{-2^k},k \geq 1</math>, bo <math>\frac{2^{-2^{k+1}}}{(2^{-2^k})^2} = \frac{2^{-2}}{2^{-2^k}}\rightarrow 0</math> – ''zbieżność kwadratowa''. | ||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
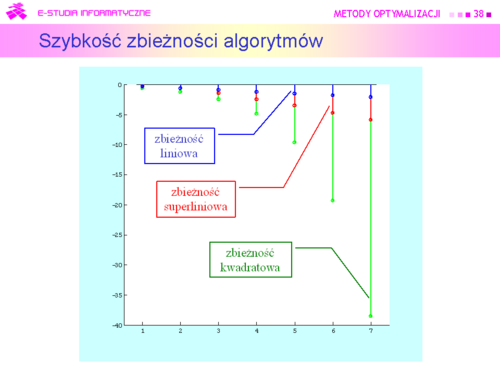
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd38.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd38.png|thumb|500px]] | ||
|valign="top"|Na rysunku przedstawiono w skali logarytmicznej siedem pierwszych wyrazów wymienionych wyżej ciągów. | |valign="top"|Na rysunku przedstawiono w skali logarytmicznej siedem pierwszych wyrazów wymienionych wyżej ciągów. | ||
| Linia 342: | Linia 339: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd40.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd40.png|thumb|500px]] | ||
|valign="top"|Pierwszy sposób został omówiony dokładnie w wykładzie poprzednim. Została pokazana ograniczoność możliwości jego stosowania. Ogólna zasada działania pozostałych trzech schematów jest taka sama i polega na naprzemiennym rozwiązywaniu dwu zadań: generacji zbioru podlegającego przeszukaniu i szukaniu w tym zbiorze punktu dającego poprawę (np. minimalizującego odpowiednio dobraną funkcję). W metodzie obszarów zaufania to zadanie poprawy jest wielowymiarową minimalizacją przy ograniczeniach, najczęściej funkcji kwadratowej. Dla metody kierunków poprawy jest to poszukiwanie punktu dającego akceptowalne zmalenie w stosunku do wartości w zerze (punkcie początkowym), odpowiednio określonej funkcji jednej zmiennej. Schematy te zostały przedstawione ogólnie i dla zastosowań praktycznych wymagają „doprecyzowania”. Zostanie to uczynione w następnych wykładach. | |valign="top"|Pierwszy sposób został omówiony dokładnie w wykładzie poprzednim. Została pokazana ograniczoność możliwości jego stosowania. Ogólna zasada działania pozostałych trzech schematów jest taka sama i polega na naprzemiennym rozwiązywaniu dwu zadań: generacji zbioru podlegającego przeszukaniu i szukaniu w tym zbiorze punktu dającego poprawę (np. minimalizującego odpowiednio dobraną funkcję). W metodzie obszarów zaufania to zadanie poprawy jest wielowymiarową minimalizacją przy ograniczeniach, najczęściej funkcji kwadratowej. Dla metody kierunków poprawy jest to poszukiwanie punktu dającego akceptowalne zmalenie w stosunku do wartości w zerze (punkcie początkowym), odpowiednio określonej funkcji jednej zmiennej. Schematy te zostały przedstawione ogólnie i dla zastosowań praktycznych wymagają „doprecyzowania”. Zostanie to uczynione w następnych wykładach. | ||
Wersja z 14:23, 5 paź 2006
 |
 |
 |
 |
 |
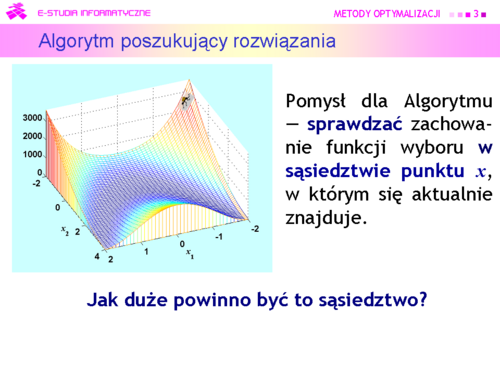
Algorytm może być:
a następnie przeszukiwać je tak jak poprzednio. |
 |
 |
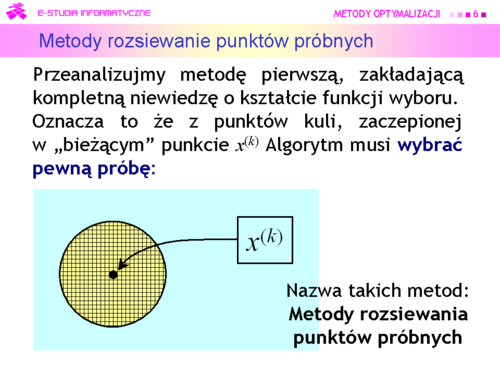
Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez:
J. A. Neldera i R. Meada i opublikowany w 1965 r. |
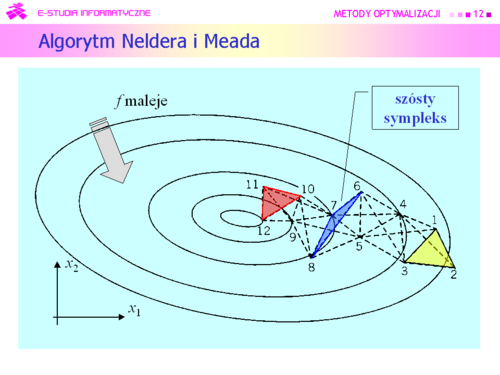 |
Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. |
 |
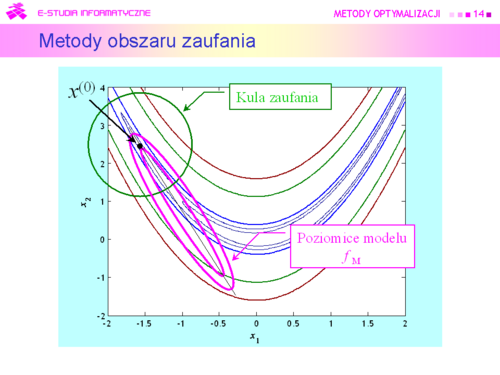
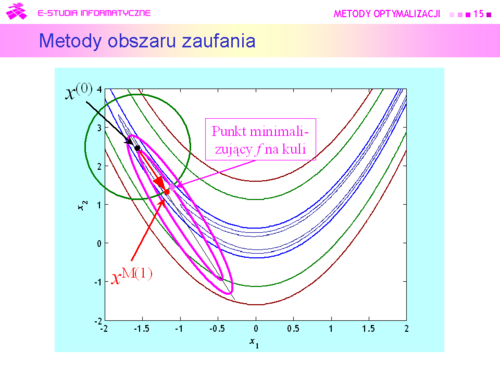
Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się:
Metodami obszaru zaufania (Trust region methods) |
 |
 |
 |
Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3).
Algorytm będzie zatem wykorzystywał: Metody kierunków poprawy |
 |
 |
 |
 |
Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający “optymalność” kolejnego punktu, a drugi określający maksymalną liczbę iteracji. |
 |
 |
 |
 |
 |
 |