|
|
| Linia 96: |
Linia 96: |
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
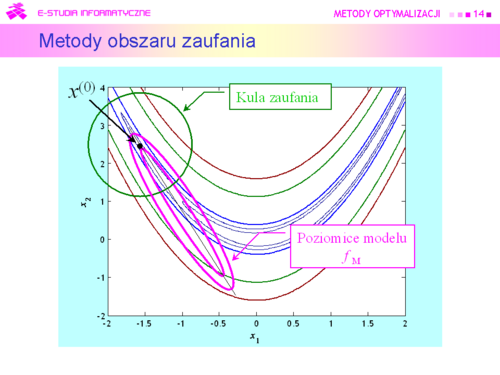
| |width="500px" valign="top"|[[Grafika:MO_M5_Slajd14.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd14.png|thumb|500px]] |
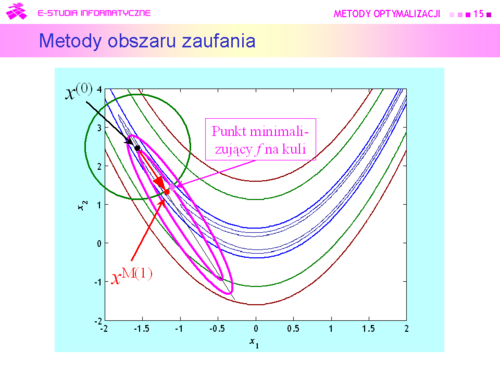
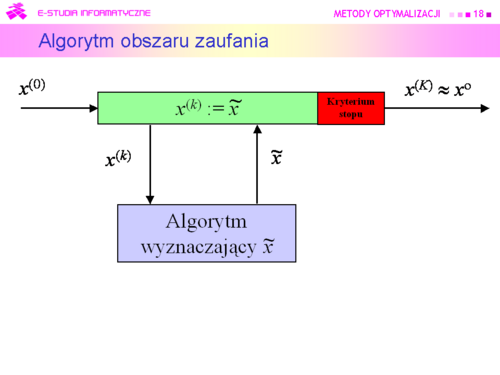
| |valign="top"|Przyjmujemy zatem, że dookoła punktu bieżącego <math>x^(k)</math> została określona kula <math>\mathbb{K}\ (x, r)</math> i funkcja <math>x \mapsto f_M(x)</math> będąca modelem zachowania się funkcji wyboru f w tej kuli, modelem dużo prostszym w analizie niż funkcja oryginalna. Do określenia modelu możemy posłużyć się intuicją opartą na rozważaniach punktu drugiego, co jak pamiętamy przekłada się na przeświadczenie, że funkcja celu dobrze daje się przybliżyć funkcją kwadratową | | |valign="top"|Przyjmujemy zatem, że dookoła punktu bieżącego <math>x^{(k)}</math> została określona kula <math>\mathbb{K}\ (x, r)</math> i funkcja <math>x \mapsto f_M(x)</math> będąca modelem zachowania się funkcji wyboru f w tej kuli, modelem dużo prostszym w analizie niż funkcja oryginalna. Do określenia modelu możemy posłużyć się intuicją opartą na rozważaniach punktu drugiego, co jak pamiętamy przekłada się na przeświadczenie, że funkcja celu dobrze daje się przybliżyć funkcją kwadratową |
|
| |
|
| <math>(APR)x \mapsto x^TQx+c^Tx+\sigma</math> | | <math>(APR)x \mapsto x^TQx+c^Tx+\sigma</math> |