MO Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 15: | Linia 15: | ||
|valign="top"|Powróćmy do naszych rozważań z części drugiej wykładu trzeciego. | |valign="top"|Powróćmy do naszych rozważań z części drugiej wykładu trzeciego. | ||
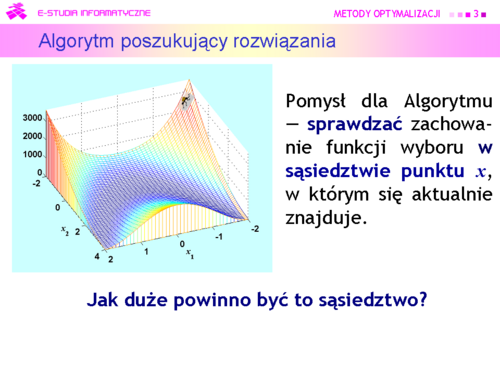
Jak pamiętamy, Algorytm jest ślepy — nie może zobaczyć rzeźby trenu na którym się znajduje. | Jak pamiętamy, Algorytm jest ślepy — nie może zobaczyć rzeźby trenu na którym się znajduje. | ||
Na schodach szedł w prawo, potem w lewo — sprawdzał swoje otoczenie. Teraz otoczenie ma więcej wymiarów, ale pomysł może być ten sam — sprawdzać zachowanie funkcji wyboru w sąsiedztwie punktu x, w którym się aktualnie znajduje. | Na schodach szedł w prawo, potem w lewo — sprawdzał swoje otoczenie. Teraz otoczenie ma więcej wymiarów, ale pomysł może być ten sam — sprawdzać zachowanie funkcji wyboru w sąsiedztwie punktu ''x'', w którym się aktualnie znajduje. | ||
Natychmiast pojawia się pytanie — jak duże powinno być to sąsiedztwo? | Natychmiast pojawia się pytanie — jak duże powinno być to sąsiedztwo? | ||
Udzielenie przemyślanej odpowiedzi nie jest zagadnieniem łatwym, ponieważ wielkość przeszukiwanego obszaru ma, intuicyjnie, wpływ, z jednej strony na szybkość znalezienia ekstremum mierzoną ilością sprawdzanych obszarów (im większy tym szybciej), a z drugiej na dokładność Algorytmu (przy ograniczonych możliwościach przeszukiwania — im mniejszy tym dokładniej). | Udzielenie przemyślanej odpowiedzi nie jest zagadnieniem łatwym, ponieważ wielkość przeszukiwanego obszaru ma, intuicyjnie, wpływ, z jednej strony na szybkość znalezienia ekstremum mierzoną ilością sprawdzanych obszarów (im większy tym szybciej), a z drugiej na dokładność Algorytmu (przy ograniczonych możliwościach przeszukiwania — im mniejszy tym dokładniej). | ||
| Linia 36: | Linia 36: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd6.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd6.png|thumb|500px]] | ||
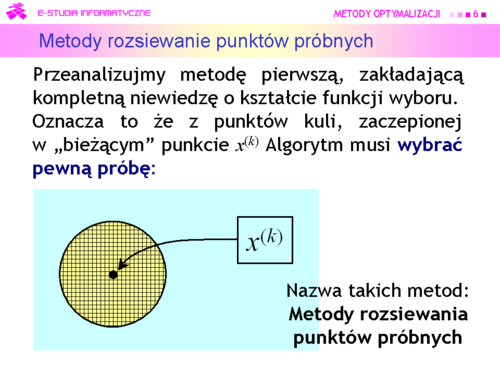
|valign="top"|Przeanalizujmy teraz sposób pierwszy, zakładający kompletną niewiedzę o kształcie funkcji wyboru. Oznacza to że z punktów kuli, zaczepionej w „bieżącym” punkcie x(k) Algorytm musi wybrać pewną próbę, np. tworząc wielowymiarową siatkę i jej węzły uznać za próbę (podejście deterministyczne), czy też wygenerować próbę losowo, bacząc aby była rozłożona równomiernie (podejście probabilistyczne). | |valign="top"|Przeanalizujmy teraz sposób pierwszy, zakładający kompletną niewiedzę o kształcie funkcji wyboru. Oznacza to że z punktów kuli, zaczepionej w „bieżącym” punkcie <math>x^{(k)}<\math> Algorytm musi wybrać pewną próbę, np. tworząc wielowymiarową siatkę i jej węzły uznać za próbę (podejście deterministyczne), czy też wygenerować próbę losowo, bacząc aby była rozłożona równomiernie (podejście probabilistyczne). | ||
|} | |} | ||
---- | ---- | ||
| Linia 44: | Linia 44: | ||
|valign="top"|Algorytm może być: | |valign="top"|Algorytm może być: | ||
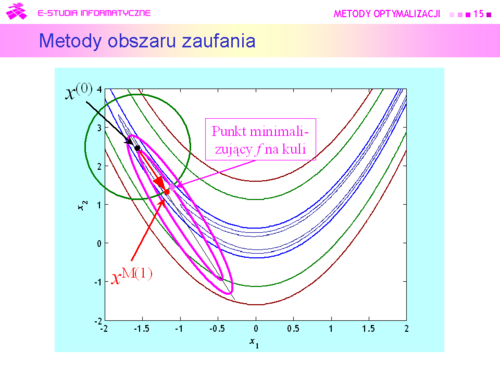
• ostrożny (wiem, że schody opadają w prawo, schodzę w prawo jeden stopień) | • ostrożny (wiem, że schody opadają w prawo, schodzę w prawo jeden stopień) | ||
–przyjąć | –przyjąć <math>x^{M(k)}<\math> za środek nowego otoczenia | ||
<math>x^{(k+1)}=x^{M(k)}=\alpha (x^{M(k)}-x^(k))+x^{(k)}, \alpha=1</math> | <math>x^{(k+1)}=x^{M(k)}=\alpha (x^{M(k)}-x^(k))+x^{(k)}, \alpha=1</math> | ||
i przeszukiwać je tak jak poprzednio. | i przeszukiwać je tak jak poprzednio. | ||
Wersja z 13:33, 3 paź 2006
 |
 |
 |
 |
 |
 |
Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez:
J. A. Neldera i R. Meada i opublikowany w 1965 r. |
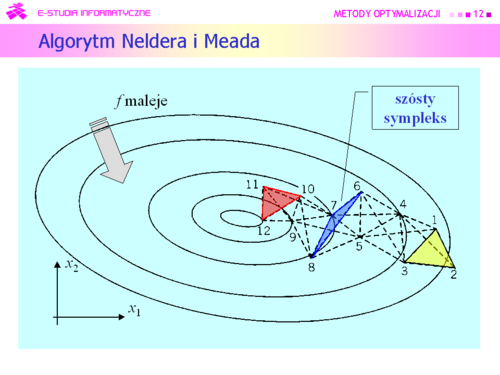 |
Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. |
 |
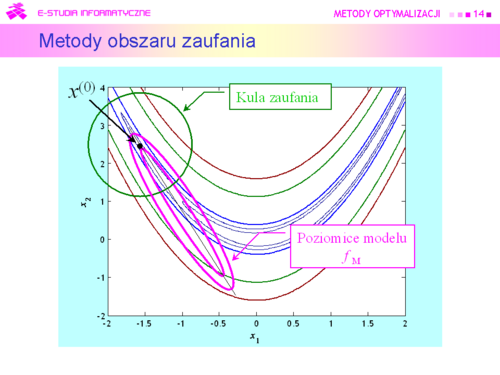
Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się:
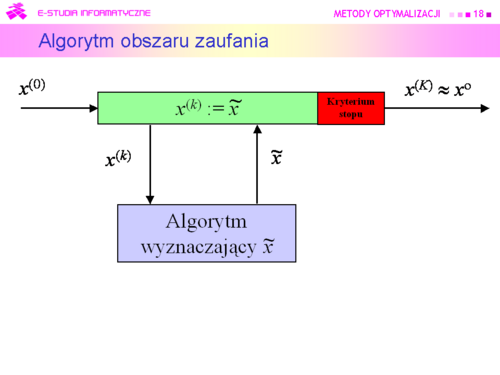
Metodami obszaru zaufania (Trust region methods) |
 |
 |
 |
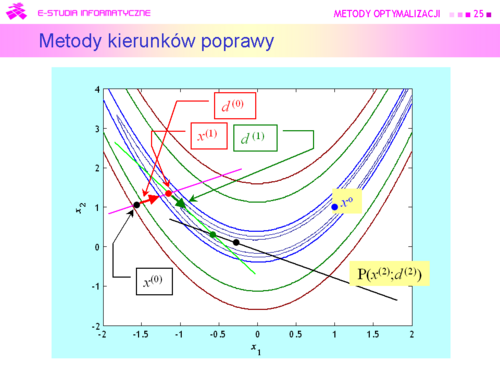
Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3).
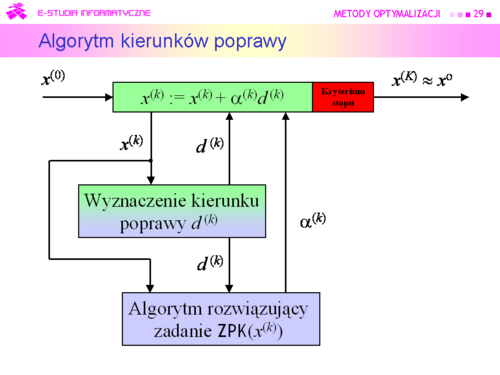
Algorytm będzie zatem wykorzystywał: Metody kierunków poprawy |
 |
 |
 |
 |
Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający “optymalność” kolejnego punktu, a drugi określający maksymalną liczbą iteracji. |
 |
 |
 |
 |
 |
 |