PF Moduł 8: Różnice pomiędzy wersjami
Nie podano opisu zmian |
mNie podano opisu zmian |
||
| Linia 203: | Linia 203: | ||
: <math>p \cdot V^\kappa=const</math>. | : <math>p \cdot V^\kappa=const</math>. | ||
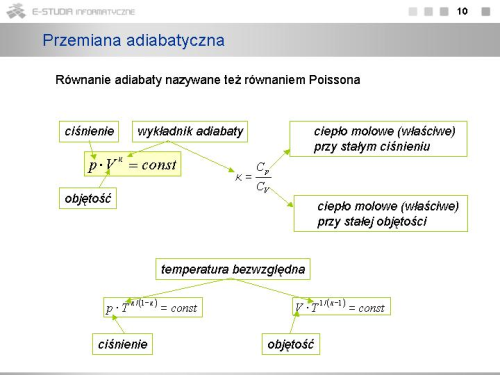
Związek ten jest równaniem adiabaty i nosi nazwę '''równania Poissona'''. Postępując podobnie można otrzymać równania określające zależności między innymi parametrami stanu dla przemiany adiabatycznej | |} | ||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:PF_M8_Slajd10.png]] | |||
|valign="top"|Związek ten jest równaniem adiabaty i nosi nazwę '''równania Poissona'''. Postępując podobnie można otrzymać równania określające zależności między innymi parametrami stanu dla przemiany adiabatycznej | |||
: <math>p \cdot T^{\kappa / (1-\kappa)}=const, \ V \cdot T^{1/(\kappa -1)}=const</math>. | : <math>p \cdot T^{\kappa / (1-\kappa)}=const, \ V \cdot T^{1/(\kappa -1)}=const</math>. | ||
| Linia 214: | Linia 220: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd11.png]] | ||
|valign="top"|Jeśli w czasie przemiany pojemność cieplna ciała pozostaje stała, czyli '''C=const''', to mówimy, że zachodzi '''przemiana politropowa'''. Znajdźmy dla gazu doskonałego związek pomiędzy ciśnieniem i objętością w takiej przemianie, czyli równanie politropy. | |valign="top"|Jeśli w czasie przemiany pojemność cieplna ciała pozostaje stała, czyli '''C=const''', to mówimy, że zachodzi '''przemiana politropowa'''. Znajdźmy dla gazu doskonałego związek pomiędzy ciśnieniem i objętością w takiej przemianie, czyli równanie politropy. | ||
| Linia 250: | Linia 256: | ||
nazywa się wykładnikiem politropy. (Pamiętajmy by nie mylić tego oznaczenia z oznaczeniem, także literą '''"n"''', liczby cząsteczek w jednostce objętości. Nie wprowadzamy tu nowych oznaczeń, by pozostać w zgodności z ogólnie przyjętym nazewnictwem.) | nazywa się wykładnikiem politropy. (Pamiętajmy by nie mylić tego oznaczenia z oznaczeniem, także literą '''"n"''', liczby cząsteczek w jednostce objętości. Nie wprowadzamy tu nowych oznaczeń, by pozostać w zgodności z ogólnie przyjętym nazewnictwem.) | ||
Można teraz obliczyć ciepło molowe '''C''' w zależności od wykładnika '''n''' | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:PF_M8_Slajd12.png]] | |||
|valign="top"|Można teraz obliczyć ciepło molowe '''C''' w zależności od wykładnika '''n''' | |||
: <math>C={n \cdot C_v - C_p \over n-1}</math>. | : <math>C={n \cdot C_v - C_p \over n-1}</math>. | ||
Wersja z 14:11, 18 wrz 2006

|
Wprowadzenie
Omówione są tu ogólne prawa makroskopowe opisujące prawidłowo zjawiska cieplne i pozwalające ilościowo przewidywać skutki różnych procesów. |

|
Zadanie 8.1
Oblicz zmianę entropii porcji moli gazu doskonałego w procesie izotermicznego rozprężania od objętości do objętości . Rozwiązanie Z pierwszej zasady termodynamiki |
Zadanie 8.2
Oblicz ciepło molowe gazu doskonałego w przemianie politropowej o równaniu
- ,
- .
W której z przemian, podczas rozszerzania, gaz ten ogrzewa się a w której oziębia?
Odpowiedź
- , oziębianie,
- , ogrzewanie.
Zadanie 8.3
Silnik cieplny pracuje według cyklu składającego się z izotermy, izobary i izochory. Objętość gazu w czasie cyklu zmienia się dziesięciokrotnie, a temperatura przemiany izotermicznej jest równa 400 K. Gazem roboczym jest 1 kmol gazu doskonałego o cząsteczkach jednoatomowych. Oblicz sprawność cyklu.
Odpowiedź
Zadanie 8.4
Oblicz zmianę entropii w cyklu Carnota.
Odpowiedź
Entropia jest funkcją stanu,
Zadanie 8.5
W naczyniu o objętości , w temperaturze , znajduje się n moli gazu rzeczywistego spełniającego równanie van der Waalsa, o znanych parametrach a, b.
- Jakie jest jego ciśnienie?
- O ile zmieni się to ciśnienie, jeśli temperatura tego gazu wzrośnie dwukrotnie przy stałej objętości?
- Odpowiedz też na powyższe pytania zakładając, że jest to gaz doskonały
Odpowiedź
, , dla gazu doskonałego a = 0 i b = 0
Słowniczek
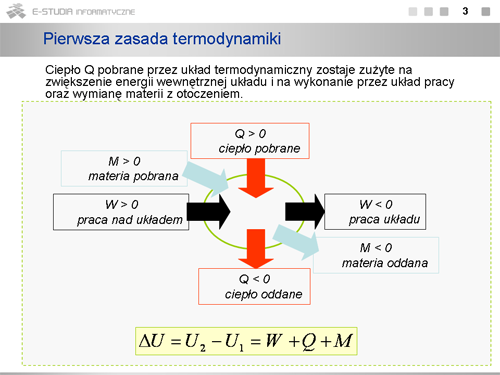
- pierwsza zasada termodynamiki - Przyrost energii wewnętrznej układu równy jest sumie dostarczonej do układu energii cieplnej, wykonanej nad układem pracy oraz energii uzyskanej wskutek wymiany materii z otoczeniem. Przyrost ten w procesach kwazistatycznych i odwracalnych nie zależy od sposobu, w jaki dokonuje się przejście, a określony jest całkowicie przez początkowy i końcowy stan układu
- pojemność cieplna - ilość ciepła potrzebna do podwyższenia temperatury ciała o jeden kelwin
- molowe ciepło właściwe - ilość ciepła potrzebna do podwyższenia temperatury jednego mola substancji o jeden kelwin
- przemiana izotermiczna - proces, który zachodzi w stałej temperaturze; T = const
- prawo Boyle'a Mariotte'a - odnosi się do przemiany izotermicznej: pV = const. W stałej temperaturze iloczyn ciśnienia i objętości jest stały lub - ciśnienie zmienia się odwrotnie proporcjonalnie do objętości.
- przemiana izochoryczna - proces, który zachodzi przy stałej objętości; V = const
- przemiana izobaryczna - proces, który zachodzi przy stałym ciśnieniu; p = const
- przemiana adiabatyczna - przemiana, która zachodzi bez wymiany ciepła z otoczeniem
- przemiana politropowa - przemiana, w czasie której pojemność cieplna ciała pozostaje stała
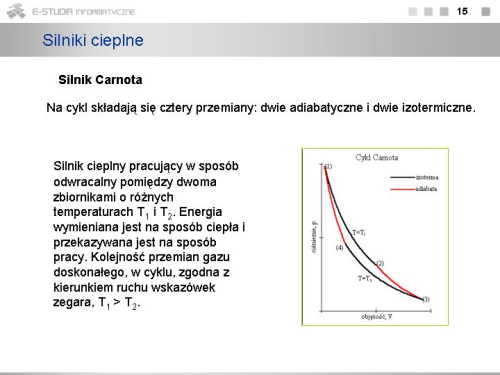
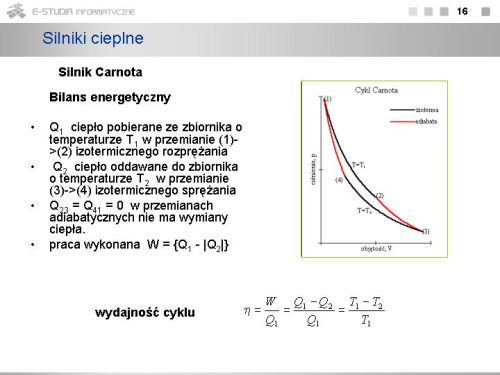
- cykl Carnota - cykl odwracalny składający się z dwóch przemian izotermicznych oraz dwóch adiabatycznych
- twierdzenia Carnota - 1. Wszystkie silniki pracujące w odwracalnym cyklu Carnota pomiędzy tymi samymi temperaturami mają tę samą sprawność.
2. Sprawność cyklu nieodwracalnego jest zawsze mniejsza od sprawności cyklu odwracalnego. - ciepło zredukowane - stosunek ilości ciepła pobranego z danego źródła do jego temperatury bezwzględnej
- entropia - 1. funkcja stanu której przyrost w przemianie odwracalnej równy jest przyrostowi ciepła zredukowanego
2. wielkość proporcjonalna do logarytmu prawdopodobieństwa termodynamicznego stanu układu - proces izoentropowy - proces, w którym entropia zachowuje wartość stałą. Procesem takim jest każdy proces adiabatyczny, odwracalny.
- nierówność Clausiusa - suma wartości ciepeł zredukowanych w każdej przemianie zamkniętej jest nie większa od zera
- prawo wzrostu entropii - Entropia układu izolowanego, w którym zachodzą procesy nieodwracalne może tylko rosnąć.
- druga zasada termodynamiki - 1. Niemożliwe jest przekazywanie ciepła przez ciało o temperaturze niższej ciału o temperaturze wyższej bez wprowadzenia innych zmian w obu ciałach i w otoczeniu
2. Niemożliwe jest pobieranie ciepła z jednego termostatu i zamiana go na pracę bez wprowadzania innych zmian w układzie i w otoczeniu.
3. Skonstruowanie perpetuum mobile drugiego rodzaju jest niemożliwe
4. Entropia układu izolowanego nie może maleć. - cykl Otta - cykl termodynamiczny składający się z dwóch adiabat i dwóch izochor. Do cyklu Otta zbliżony jest cykl pracy silnika benzynowego.
- cykl Diesla - cykl termodynamiczny składający się z dwóch adiabat izochory i izobary. Opisuje pracę silnika Diesla.
- równanie van der Waalsa - równanie stanu gazu rzeczywistego biorące pod uwagę objętość cząsteczek gazu i siły ich wzajemnych oddziaływań
- stan (punkt) krytyczny - stan, w którym znikają różnice pomiędzy własnościami cieczy, pary nasyconej i gazu. Gęstości substancji w tych trzech stanach są jednakowe.
- wartości krytyczne - wartości ciśnienia, temperatury i gęstości w punkcie krytycznym
- faza substancji - stan substancji charakteryzujący się jednoznacznie określonymi własnościami
- przejście fazowe - proces w rezultacie którego zmienia się faza substancji
- parowanie - proces polegający na przejściu z fazy ciekłej do gazowej
- skraplanie - proces polegający na przejściu z fazy gazowej do fazy ciekłej
- sublimacja - proces polegający na przejściu z fazy gazowej do fazy stałej
- stan równowagi dynamicznej - stan którego własności makroskopowe nie zmieniają się w czasie pomimo zachodzących procesów w skali mikroskopowej
- anizotropia - zależność własności fizycznych ciała od kierunku
- stan metastabilny - stan układu, który może być zmieniony wskutek bardzo niewielkiego zaburzenia warunków w jakich układ się znajduje
- para nasycona - para o maksymalnej możliwej gęstości w danej temperaturze
- para przesycona - metastabilny stan pary, w warunkach ciśnienia i temperatury odpowiadających stanowi ciekłemu danej substancji
- ciecz przegrzana - metastabilny stan cieczy, w warunkach ciśnienia i temperatury odpowiadających stanowi gazowemu danej substancji
- punkt potrójny - punkt określający warunki ciśnienia i temperatury, w których mogą istnieć w równowadze trzy stany skupienia danej substancji: stała, ciekła i gazowa
- wykres stanu - wykres we współrzędnych temperatury i ciśnienia określający warunki współistnienia faz danej substancji