PF Moduł 10: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 46: | Linia 46: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M10_Slajd4.png]] | |width="450px" valign="top"|[[Grafika:PF_M10_Slajd4.png]][[Grafika:PF_M10_Slajd5.png]] | ||
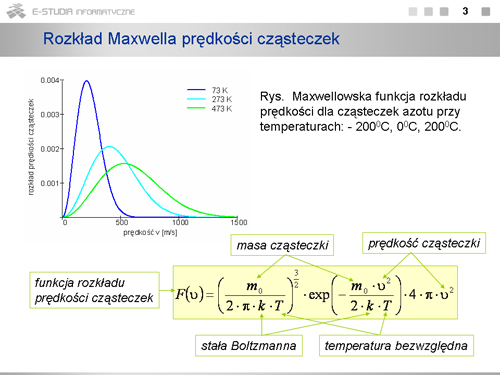
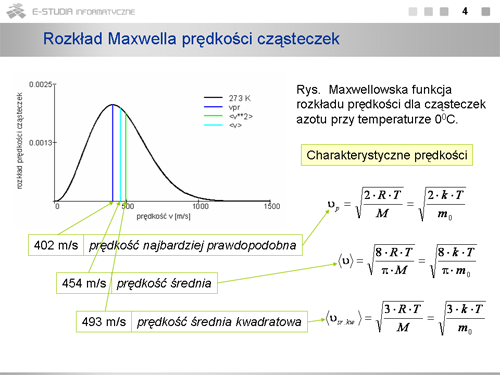
|valign="top"|Dla każdej temperatury można określić prędkość, która występuje najczęściej, czyli najwięcej cząsteczek ma prędkości bliskie tej wartości. Wartość ta odpowiada maksimum rozkładu Maxwella. Prędkość tę nazywamy prędkością najbardziej prawdopodobną, <math>v_p\,</math> . Można ją określić z matematycznego warunku na maksimum funkcji. | |valign="top"|Dla każdej temperatury można określić prędkość, która występuje najczęściej, czyli najwięcej cząsteczek ma prędkości bliskie tej wartości. Wartość ta odpowiada maksimum rozkładu Maxwella. Prędkość tę nazywamy prędkością najbardziej prawdopodobną, <math>v_p\,</math> . Można ją określić z matematycznego warunku na maksimum funkcji. | ||
| Linia 60: | Linia 60: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika: | |width="450px" valign="top"|[[Grafika:PF_M10_Slajd6.png]]][[Grafika:PF_M10_Slajd7.png]] | ||
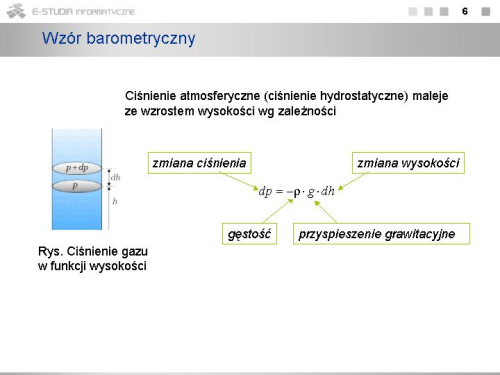
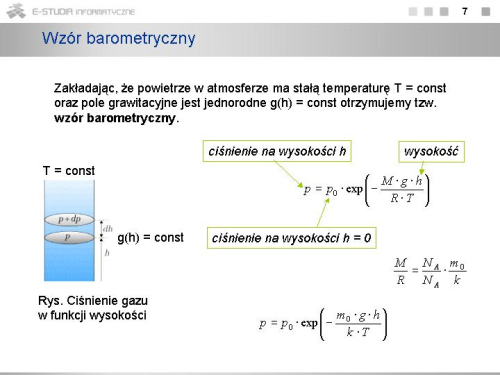
|valign="top"|Ciśnienie atmosferyczne w danym punkcie nad powierzchnią Ziemi określone jest przez ciężar warstwy powietrza leżącej powyżej tego punktu, powinno zależeć od wysokości. Im większa wysokość, tym mniejsza jest warstwa powietrza, więc i ciśnienie jest mniejsze. Różnica ciśnień <math>dp\,</math> związana ze wzrostem wysokości <math>dh\,</math> ma znak ujemny i wynosi | |valign="top"|Ciśnienie atmosferyczne w danym punkcie nad powierzchnią Ziemi określone jest przez ciężar warstwy powietrza leżącej powyżej tego punktu, powinno zależeć od wysokości. Im większa wysokość, tym mniejsza jest warstwa powietrza, więc i ciśnienie jest mniejsze. Różnica ciśnień <math>dp\,</math> związana ze wzrostem wysokości <math>dh\,</math> ma znak ujemny i wynosi | ||
| Linia 106: | Linia 107: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika: | |width="450px" valign="top"|[[Grafika:PF_M10_Slajd8.png]]][[Grafika:PF_M10_Slajd9.png]] | ||
|valign="top"|W rozważaniach dotyczących rozkładu Maxwella ignorowaliśmy całkowicie fakt, że cząsteczki poruszają się w polu sił ciężkości, a więc wyróżniony jest kierunek pionowy. Wzór barometryczny wskazuje, że ciężar cząsteczek ma wpływ na rozkład ciśnienia w funkcji wysokości. Jak uwzględnić ten efekt w opisie rozkładu prędkości cząsteczek? | |valign="top"|W rozważaniach dotyczących rozkładu Maxwella ignorowaliśmy całkowicie fakt, że cząsteczki poruszają się w polu sił ciężkości, a więc wyróżniony jest kierunek pionowy. Wzór barometryczny wskazuje, że ciężar cząsteczek ma wpływ na rozkład ciśnienia w funkcji wysokości. Jak uwzględnić ten efekt w opisie rozkładu prędkości cząsteczek? | ||
| Linia 124: | Linia 126: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M10_Slajd8.png]][[Grafika: | |width="450px" valign="top"|[[Grafika:PF_M10_Slajd8.png]][[Grafika:PF_M10_Slajd10.png]] | ||
|valign="top"|Stan układu określany przez parametry makroskopowe, jak temperatura, ciśnienie, energia wewnętrzna, itd. nazywamy '''''makrostanem'''''. Stan układu wyznaczony przez określenie stanów wszystkich cząsteczek wchodzących w jego skład nazywamy '''''mikrostanem'''''. Liczba możliwych mikrostanów odpowiadających danemu makrostanowi jest na ogół ogromna, analiza nasza będzie mieć charakter statystyczny. Liczba mikrostanów odpowiadających danemu makrostanowi nazywa się '''''prawdopodobieństwem termodynamicznym''''' lub '''''wagą statystyczną''''' makrostanu. | |valign="top"|Stan układu określany przez parametry makroskopowe, jak temperatura, ciśnienie, energia wewnętrzna, itd. nazywamy '''''makrostanem'''''. Stan układu wyznaczony przez określenie stanów wszystkich cząsteczek wchodzących w jego skład nazywamy '''''mikrostanem'''''. Liczba możliwych mikrostanów odpowiadających danemu makrostanowi jest na ogół ogromna, analiza nasza będzie mieć charakter statystyczny. Liczba mikrostanów odpowiadających danemu makrostanowi nazywa się '''''prawdopodobieństwem termodynamicznym''''' lub '''''wagą statystyczną''''' makrostanu. | ||
| Linia 138: | Linia 140: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika: | |width="450px" valign="top"|[[Grafika:PF_M10_Slajd11.png]] | ||
|valign="top"|Dla zilustrowania tych relacji przeanalizujmy szczegółowo przypadek małej liczby cząsteczek, na przykład - czterech. W lewej kolumnie tabeli wymienione są możliwe '''makrostany''' układu. | |valign="top"|Dla zilustrowania tych relacji przeanalizujmy szczegółowo przypadek małej liczby cząsteczek, na przykład - czterech. W lewej kolumnie tabeli wymienione są możliwe '''makrostany''' układu. | ||
| Linia 149: | Linia 151: | ||
Jest to właśnie waga statystyczna danego makrostanu. Sumaryczna liczba wszystkich mikrostanów wynosi <math>2^N\,</math>. Prawdopodobieństwo danego makrostanu jest równe stosunkowi jego wagi statystycznej do sumarycznej liczby wszystkich mikrostanów i dla naszego przypadku podane jest w prawej kolumnie tabeli. Prawdopodobieństwo, że dana cząsteczka znajdzie się z prawej lub z lewej strony naczynia jest takie samo, czyli '''prawdopodobieństwa wszystkich mikrostanów są sobie równe'''. Uogólnienie tego stwierdzenia na zdefiniowane w dowolny sposób mikrostany nosi nazwę '''hipotezy ergodycznej'''. | Jest to właśnie waga statystyczna danego makrostanu. Sumaryczna liczba wszystkich mikrostanów wynosi <math>2^N\,</math>. Prawdopodobieństwo danego makrostanu jest równe stosunkowi jego wagi statystycznej do sumarycznej liczby wszystkich mikrostanów i dla naszego przypadku podane jest w prawej kolumnie tabeli. Prawdopodobieństwo, że dana cząsteczka znajdzie się z prawej lub z lewej strony naczynia jest takie samo, czyli '''prawdopodobieństwa wszystkich mikrostanów są sobie równe'''. Uogólnienie tego stwierdzenia na zdefiniowane w dowolny sposób mikrostany nosi nazwę '''hipotezy ergodycznej'''. | ||
Najbardziej prawdopodobne są makrostany, w których po obu stronach znajduje się ta sama liczba cząsteczek. Gdybyśmy w stanie początkowym umieścili gaz z jednej strony naczynia, to po pewnym czasie cząsteczki zajęłyby pozycje odpowiadające największej wadze statystycznej, czyli największemu prawdopodobieństwu termodynamicznemu. Stan taki nazywamy '''stanem równowagi'''. Układ wyprowadzony ze stanu równowagi ma tendencję do samorzutnego powrotu do tego stanu. Inne stany układu są mniej prawdopodobne. Proces zmierzający do ustalenia się w układzie stanu równowagi jest procesem nieodwracalnym, bowiem proces do niego odwrotny jest bardzo mało prawdopodobny. Możemy wiec powiedzieć, że '''dany proces jest wtedy nieodwracalny, gdy proces do niego odwrotny jest bardzo mało prawdopodobny'''. | |} | ||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M10_Slajd12.png]] | |||
|valign="top"|Najbardziej prawdopodobne są makrostany, w których po obu stronach znajduje się ta sama liczba cząsteczek. Gdybyśmy w stanie początkowym umieścili gaz z jednej strony naczynia, to po pewnym czasie cząsteczki zajęłyby pozycje odpowiadające największej wadze statystycznej, czyli największemu prawdopodobieństwu termodynamicznemu. Stan taki nazywamy '''stanem równowagi'''. Układ wyprowadzony ze stanu równowagi ma tendencję do samorzutnego powrotu do tego stanu. Inne stany układu są mniej prawdopodobne. Proces zmierzający do ustalenia się w układzie stanu równowagi jest procesem nieodwracalnym, bowiem proces do niego odwrotny jest bardzo mało prawdopodobny. Możemy wiec powiedzieć, że '''dany proces jest wtedy nieodwracalny, gdy proces do niego odwrotny jest bardzo mało prawdopodobny'''. | |||
|} | |} | ||
| Linia 156: | Linia 164: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika: | |width="450px" valign="top"|[[Grafika:PF_M10_Slajd13.png]] | ||
|valign="top"|Kiedy układ składa się z nie oddziałujących podukładów wówczas prawdopodobieństwo stanu równe jest iloczynowi prawdopodobieństw stanów podukładów. | |valign="top"|Kiedy układ składa się z nie oddziałujących podukładów wówczas prawdopodobieństwo stanu równe jest iloczynowi prawdopodobieństw stanów podukładów. | ||
| Linia 173: | Linia 181: | ||
gdzie <math>k\,</math> jest znaną nam już stałą Boltzmanna. Entropia rośnie wraz ze wzrostem prawdopodobieństwa stanu układu, jest logarytmiczną miarą tego prawdopodobieństwa. | gdzie <math>k\,</math> jest znaną nam już stałą Boltzmanna. Entropia rośnie wraz ze wzrostem prawdopodobieństwa stanu układu, jest logarytmiczną miarą tego prawdopodobieństwa. | ||
Wymieńmy podstawowe własności entropii wynikające z naszych wcześniejszych rozważań. | |} | ||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M10_Slajd14.png]] | |||
|valign="top"|Wymieńmy podstawowe własności entropii wynikające z naszych wcześniejszych rozważań. | |||
1. ''Przemiany nieodwracalne zachodzące w układzie izolowanym prowadzą do wzrostu entropii układu''. Prawo to wyraża wzór <math>dS>0\,</math> . | 1. ''Przemiany nieodwracalne zachodzące w układzie izolowanym prowadzą do wzrostu entropii układu''. Prawo to wyraża wzór <math>dS>0\,</math> . | ||
| Linia 189: | Linia 203: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika: | |width="450px" valign="top"|[[Grafika:PF_M10_Slajd15.png]] | ||
|valign="top"|'''Zadanie 10.4''' | |valign="top"|'''Zadanie 10.4''' | ||
Przy jakiej temperaturze średnia prędkość kwadratowa cząsteczek dwutlenku węgla będzie równa średniej prędkości kwadratowej cząsteczek azotu w temperaturze <math>0^\circ C</math>? | Przy jakiej temperaturze średnia prędkość kwadratowa cząsteczek dwutlenku węgla będzie równa średniej prędkości kwadratowej cząsteczek azotu w temperaturze <math>0^\circ C</math>? | ||
Odpowiedź | |||
Przy temperaturze <math>429\, K\,</math>. | Przy temperaturze <math>429\, K\,</math>. | ||
| Linia 201: | Linia 215: | ||
Izolowany układ dwóch zbiorników. Zbiornik o objętości <math>V_1\,</math> zawierał <math>n_{M1}\,</math> moli gazu o temperaturze <math>T\,</math> . Zbiornik o objętości <math>V_2\,</math> zawierał <math>n_{M2}\,</math> moli również o temperaturze <math>T\,</math> , Oblicz zmianę entropii tych gazów po połączeniu zbiorników i powstaniu mieszaniny. | Izolowany układ dwóch zbiorników. Zbiornik o objętości <math>V_1\,</math> zawierał <math>n_{M1}\,</math> moli gazu o temperaturze <math>T\,</math> . Zbiornik o objętości <math>V_2\,</math> zawierał <math>n_{M2}\,</math> moli również o temperaturze <math>T\,</math> , Oblicz zmianę entropii tych gazów po połączeniu zbiorników i powstaniu mieszaniny. | ||
Odpowiedź | Odpowiedź | ||
Wersja z 15:21, 15 wrz 2006
Słowniczek
| wzór barometryczny | podaje zależność ciśnienia atmosferycznego od wysokości nad powierzchnią Ziemi |
| rozkład Maxwella prędkości cząsteczek | rozkład wartości prędkości chaotycznego ruchu cząsteczek gazu doskonałego dla zadanej temperatury i masy cząsteczek |
| rozkład Boltzmanna | rozkład koncentracji cząsteczek w funkcji ich wysokości lub energii potencjalnej. Odnosi się nie tylko do pola sił przyciągania ziemskiego, ale do dowolnego pola potencjalnego, jeśli tylko cząsteczki poruszają się chaotycznym ruchem cieplnym. |
| mikrostan | stan układu w którym opisane są stany wszystkich jego elementów |
| hipoteza ergodyczna | Prawdopodobieństwa wszystkich mikrostanów są jednakowe |
| makrostan | stan układu opisany za pomocą wielkości odnoszących się do całości układu |
| prawdopodobieństwo termodynamiczne (waga statystyczna) | odnosi się do makrostanu układu: liczba mikroskoopowych sposobów realizacji danego makrostanu (liczba mikrostanów odpowiadająca danemu makrostanowi) |
| entropia | definicja statystyczna: wielkość proporcjonalna do logarytmu prawdopodobieństwa termodynamicznego stanu układu |
| fluktuacje | losowe odchylenia danej wielkości od wartości średniej |
| prawo wzrostu entropii | entropia układu izolowanego nie może maleć, w procesach nieodwracalnych entropia układu rośnie |